题目内容
14.用反证法证明命题“若正整数a,b,c满足b2-2ac=0,则a,b,c中至少有一个是偶数”时,反设应为假设a,b,c都是奇数.分析 利用反证法证明的步骤,从问题的结论的反面出发否定即可.
解答 解:假设a,b,c都是奇数“至少有一个偶数”的否定为“都不是偶数”,即反设应为“假设a,b,c都是奇数”.
故答案为:假设a,b,c都是奇数.
点评 此题主要考查了反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知在等比数列{an}中,a3+a6=6,a6+a9=$\frac{3}{4}$,则a8+a11等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{3}{32}$ |
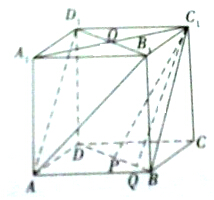 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.