题目内容
已知M(-5,0),N(5,0)是平面上的两点,若曲线C上至少存在一点P,使|PM|=|PN|+6,则称曲线C为“黄金曲线”.下列五条曲线:
①
-
=1;
②
+
=1;
③
-
=1;
④y2=4x;
⑤x2+y2-2x-3=0
其中为“黄金曲线”的是 .(写出所有“黄金曲线”的序号)
①
| y2 |
| 16 |
| x2 |
| 9 |
②
| x2 |
| 4 |
| y2 |
| 9 |
③
| x2 |
| 4 |
| y2 |
| 9 |
④y2=4x;
⑤x2+y2-2x-3=0
其中为“黄金曲线”的是
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据双曲线的定义,可得点P的轨迹是以M、N为焦点,2a=6的双曲线,由此算出所求双曲线的方程.再分别将双曲线与五条曲线联立,通过解方程判断是否有交点,由此可得答案.
解答:
解:∵点M(-5,0),N(5,0),点P使|PM|-|PN|=6,
∴点P的轨迹是以M、N为焦点,2a=6的双曲线,
可得b2=c2-a2=52-32=16,
则双曲线的方程为
-
=1(x>0),
对于①,两方程联立,无解.则①错;
对于②,联立
+
=1和
-
=1(x>0),无解,则②错;
对于③,联立
-
=1和
-
=1(x>0),无解,则②错;
对于④,联立y2=4x和
-
=1(x>0),解得x=
成立.
对于⑤,联立x2+y2-2x-3=0和
-
=1(x>0),化简得25x2-18x-171=0,
由韦达定理可得两根之积小于0,必有一个正根,则⑤成立.
故答案为:④⑤.
∴点P的轨迹是以M、N为焦点,2a=6的双曲线,
可得b2=c2-a2=52-32=16,
则双曲线的方程为
| x2 |
| 9 |
| y2 |
| 16 |
对于①,两方程联立,无解.则①错;
对于②,联立
| x2 |
| 4 |
| y2 |
| 9 |
| x2 |
| 9 |
| y2 |
| 16 |
对于③,联立
| x2 |
| 4 |
| y2 |
| 9 |
| x2 |
| 9 |
| y2 |
| 16 |
对于④,联立y2=4x和
| x2 |
| 9 |
| y2 |
| 16 |
9+3
| ||
| 8 |
对于⑤,联立x2+y2-2x-3=0和
| x2 |
| 9 |
| y2 |
| 16 |
由韦达定理可得两根之积小于0,必有一个正根,则⑤成立.
故答案为:④⑤.
点评:本题考查双曲线的定义和方程,考查联立曲线方程求交点,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
设a,b,c分别是△ABC中∠A,∠B,∠C所对边的边长,则直线sinA•x-ay-c=0与bx+sinB•y+sinC=0的位置关系是( )
| A、平行 | B、重合 |
| C、垂直 | D、相交但不垂直 |
已知集合A={cos0°,sin270°},B={x|x2+x=0},则A∩B为( )
| A、{0,-1} | B、{-1,1} |
| C、{-1} | D、{0} |
双曲线
-
=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
| y2 |
| a2 |
| x2 |
| b2 |
| A、(1,2] |
| B、(1,2) |
| C、(2,+∞) |
| D、[2,+∞) |
定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,给出下列四个命题: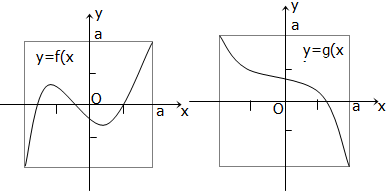
(1)方程f[g(x)]=0有且仅有三个解;
(2)方程g[f(x)]=0有且仅有三个解;
(3)方程f[f(x)]=0有且仅有九个解;
(4)方程g[g(x)]=0有且仅有一个解.
那么,其中正确命题的个数是( )

(1)方程f[g(x)]=0有且仅有三个解;
(2)方程g[f(x)]=0有且仅有三个解;
(3)方程f[f(x)]=0有且仅有九个解;
(4)方程g[g(x)]=0有且仅有一个解.
那么,其中正确命题的个数是( )
| A、(1)(4) |
| B、(2)(3) |
| C、(1)(3) |
| D、(2)(4) |
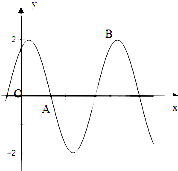 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(| π |
| 3 |
| 13π |
| 12 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、命题“?x∈R使得x2+x+1<0”的否定是“?x∈R均有x2+x+1<0” |