题目内容
13.(x-$\frac{1}{{x}^{2}}$)9的展开式中系数最大的项为$\frac{126}{{x}^{3}}$.分析 利用二项展开式的通项公式求出通项,求出正的系数,选出最大值.
解答 解:(x-$\frac{1}{{x}^{2}}$)9的展开式的通项为Tr+1=(-1)rC9rx9-3r,
∴展开式中系数最大的是当r=4时,
∴系数最大的项是第五项为T5=C94•x-3=$\frac{126}{{x}^{3}}$,
故答案为:$\frac{126}{{x}^{3}}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属基础题.

练习册系列答案
相关题目
10.设函数f(x)=2${\;}^{\sqrt{|x|+1}}$-$\frac{3}{1+{x}^{2}}$,则使得f(x2+$\frac{2}{3}$x+2)>f(-x2+x-1)成立的x的取值范围是( )
| A. | [-$\frac{3}{5}$,+∞) | B. | (-∞,$\frac{3}{5}$] | C. | (-$\frac{3}{5}$,+∞) | D. | $({-\frac{3}{5},\frac{3}{5}})$ |
8.已知等差数列{an}的前15项之和为$\frac{15π}{4}$,则tan(a7+a8+a9)=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
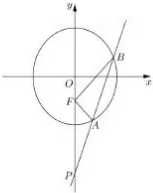 如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P
如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P