题目内容
3.化简:(1)$\frac{cosα}{1-sinα}$=$\frac{1+sinα}{cosα}$;
(2)$\frac{tanαsinα}{tanα-sinα}$=$\frac{tanα+sinα}{tanαsinα}$.
分析 (1)法一,利用sin2 α+cos2 α=1得出(1-sinα)(1+sinα)=cosα•cosα,从而证明等式成立;
法二,证明$\frac{cosα}{1-sinα}$-$\frac{1+sinα}{cosα}$=0,即可证明等式成立;
(2)利用作差法,证明$\frac{tanαsinα}{tanα-sinα}$-$\frac{tanα+sinα}{tanαsinα}$=0,即可证明等式成立.
解答 解:(1)法一:由sin2 α+cos2 α=1得,
1-sin2 α=cos2 α,即(1-sinα)(1+sinα)=cosα•cosα
∴$\frac{cosα}{1-sinα}$=$\frac{1+sinα}{cosα}$.
法二:$\frac{cosα}{1-sinα}$-$\frac{1+sinα}{cosα}$=$\frac{cosα•cosα-(1+sinα)(1-sinα)}{(1-sinα)cosα}$
=$\frac{{cos}^{2}α-1{+sin}^{2}α}{(1-sinα)cosα}$
=$\frac{1-1}{(1-sinα)cosα}$=0,
∴$\frac{cosα}{1-sinα}$=$\frac{1+sinα}{cosα}$;
(2)∵$\frac{tanαsinα}{tanα-sinα}$-$\frac{tanα+sinα}{tanαsinα}$=$\frac{\frac{sinα}{cosα}•sinα}{\frac{sinα}{cosα}-sinα}$-$\frac{\frac{sinα}{cosα}+sinα}{\frac{sinα}{cosα}•sinα}$
=$\frac{sinα}{1-cosα}$-$\frac{1+cosα}{sinα}$
=$\frac{{sin}^{2}α-(1+cosα)(1-cosα)}{(1-cosα)sinα}$
=$\frac{{sin}^{2}α-1{+cos}^{2}α}{(1-cosα)sinα}$
=$\frac{1-1}{(1-cosα)sinα}$=0,
∴$\frac{tanαsinα}{tanα-sinα}$=$\frac{tanα+sinα}{tanαsinα}$.
点评 本题考查了同角的三角函数基本关系的应用问题,也考查了逻辑推理能力与运算能力的应用问题,是基础题目.

| A. | 第6项 | B. | 第7项 | C. | 第11项 | D. | 第6项和第7项 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
 如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.
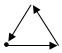
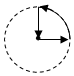
如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.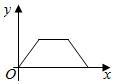 如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )
如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )

 图是一个商场某段时间制定销售计划时的局部结构图,从图中可以看出“计划”的制定主要受( )个因素的影响.
图是一个商场某段时间制定销售计划时的局部结构图,从图中可以看出“计划”的制定主要受( )个因素的影响.