题目内容
7.已知函数f(x)=-x3+ax2-x-1在R上不是单调函数,则实数a的取值范围是( )| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |
分析 求导数得到f′(x)=-3x2+2ax-1,根据f(x)在R上不是单调函数即可得出△=4a2-12>0,解该不等式即可得出实数a的取值范围.
解答 解:f′(x)=-3x2+2ax-1;
∵f(x)在R上不是单调函数;
∴f′(x)=0有两个不同实数根;
∴△=4a2-12>0;
解得$a<-\sqrt{3}$,或a$>\sqrt{3}$;
∴实数a的取值范围是$(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$.
故选:C.
点评 考查根据导数符号判断函数单调性的方法,熟悉二次函数的图象,清楚一元二次方程的实根情况和判别式△取值的关系.

练习册系列答案
相关题目
17.设{an}是递增等差数列,前三项的和是12,前三项的积为48,则a3=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
18.如图所示,运行流程图,则输出的n的值等于( )
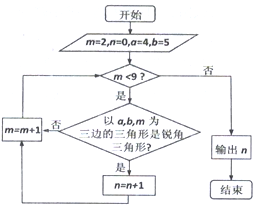

| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
12. 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线; ②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
19.已知函数f(x)=sin(ωx+$\frac{π}{8}$)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
| A. | 向左平移$\frac{3π}{4}$个单位长度 | B. | 向右平移$\frac{3π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{3π}{16}$个单位长度 | D. | 向右平移$\frac{3π}{16}$个单位长度 |
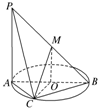 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题: