题目内容
以两条坐标轴为对称轴的椭圆过点P（
，-4）和Q（-
，3），则此椭圆的方程是（ ）
| 3 |
| 5 |
| 4 |
| 5 |
A、
| ||||
B、x2+
| ||||
C、
| ||||
| D、以上均不对 |
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：设经过两点P（
，-4）和Q（-
，3），的椭圆标准方程为mx2+ny2=1（m＞0，n＞0，m≠n），利用待定系数法能求出椭圆方程．
| 3 |
| 5 |
| 4 |
| 5 |
解答：
解：设经过两点P（
，-4）和Q（-
，3），的椭圆标准方程为mx2+ny2=1（m＞0，n＞0，m≠n），
代入A、B得，
，解得m=1，n=
，
∴所求椭圆方程为x2+
=1．
故选：B．
| 3 |
| 5 |
| 4 |
| 5 |
代入A、B得，
|
| 1 |
| 25 |
∴所求椭圆方程为x2+
| y2 |
| 25 |
故选：B．
点评：本题考查椭圆标准方程的求法，是中档题，解题时要认真审题，注意椭圆简单性质的合理运用．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知等比数列{an}各项都为正数，并且有a2•a9=4，则log2a1+log2a2+…+log2a10的值为（ ）
| A、10 | B、20 | C、30 | D、40 |
函数f（x）=e
的定义域是（ ）
| x2-1 |
| A、[-1，1] |
| B、[1，+∞） |
| C、（-∞，-1] |
| D、（-∞，-1]∪[1，+∞） |
定义一种运算（a，b）*（c，d）=ac+bd，若函数f（x）=（1，log5x）*（（
）x，log2
），x0是方程f（x）=0的解，且x1＞x0，则f（x1）的值（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、恒为正值 | B、等于零 |
| C、恒为负值 | D、不小于0 |
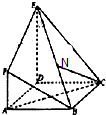如图，多面体EFABCD中，底面ABCD是正方形，AF⊥平面ABCD，DF∥AF，AB=DE=2，AF=1．