题目内容
13．如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是20+$4\sqrt{2}$cm2．
分析 由三视图还原原几何体，可得原几何体为组合体，下面是棱长为2的正方体，上面是正四棱锥，正四棱锥的高是1．求出上面四棱锥的斜高，则表面积可求．
解答 解：由三视图还原原几何体如图，
几何体为组合体，下面是棱长为2的正方体，上面是正四棱锥，正四棱锥的高是1．
则正四棱锥的斜高为$\sqrt{2}$．
∴组合体的表面积为$5×2×2+4×\frac{1}{2}×2×\sqrt{2}=20+4\sqrt{2}$（cm2）．
故答案为：20+4$\sqrt{2}$．
点评 本题考查由三视图求几何体的体积，考查空间想象能力和思维能力，关键是由三视图还原原几何体，是中档题．
练习册系列答案
相关题目
20．
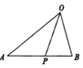如图，在△OAB，点P在边AB上，且AP：PB=5：3，则$\overrightarrow{OP}$=（ ）
如图，在△OAB，点P在边AB上，且AP：PB=5：3，则$\overrightarrow{OP}$=（ ）| A． | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B． | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C． | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D． | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
8．某四棱锥的三视图如图所示，该四棱锥外接球的体积为（ ）
| A． | $\frac{{\sqrt{6}}}{3}π$ | B． | $\frac{{\sqrt{6}}}{2}π$ | C． | $\sqrt{6}π$ | D． | $3\sqrt{6}π$ |
18．某同学在利用“五点法”作函数f（x）=Asin（ωx+Φ）+t的图象时，列出了如下表格中的部分数据
（1）请将表格补充完整，并写出f（x）的解析式；
（2）若x∈[-$\frac{5π}{12}，\frac{π}{4}}$]，求f（x）的最大值和最小值．
| x | $\frac{5π}{12}$ | $\frac{3π}{4}$ | |||
| ωx+Φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f（x） | 6 | -2 |
（2）若x∈[-$\frac{5π}{12}，\frac{π}{4}}$]，求f（x）的最大值和最小值．
5．某班级有一个学生A在操场上绕圆形跑道逆时针方向匀速跑步，每52秒跑一圈，在学生A开始跑步时，在教室内有一个学生B往操场看了一次，以后每50秒往操场上看一次，则该学生B“感觉”到学生A的运动是（ ）
| A． | 逆时针方向匀速前跑 | B． | 顺时针方向匀速前跑 | ||
| C． | 顺时针方向匀速后退 | D． | 静止不动 |
2．某校为了解高二年级不同性别的学生对取消艺术课的态度（支持或反对）进行了如下的调查研究．全年级共有1350人，男女生比例为8：7，现按分层抽样方法抽取若干名学生，每人被抽到的概率均为$\frac{1}{9}$，通过对被抽取学生的问卷调查，得到如下2×2列联表：
（1）完成下列联表，并判断能否有99%的把握认为态度与性别有关？
（2）若某班有6名男生被抽到，其中2人支持，4人反对；有4名女生被抽到，其中2人支持，2人反对，现从这10人中随机抽取一男一女进一步调查原因．求其中恰有一人支持一人反对的概率．
参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+c）（b+d）（a+b）（c+d）}$
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
（2）若某班有6名男生被抽到，其中2人支持，4人反对；有4名女生被抽到，其中2人支持，2人反对，现从这10人中随机抽取一男一女进一步调查原因．求其中恰有一人支持一人反对的概率．
参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+c）（b+d）（a+b）（c+d）}$
| P（K2≥k0） | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.7069% | 3.841 | 6.635 | 7.879 | 10.828 |