题目内容
15.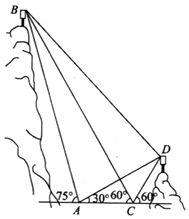 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
分析 在△ACD中,∠DAC=30°推断出CD=AC,同时根据CB是△CAD底边AD的中垂线,判断出BD=BA,进而在△ABC中利用余弦定理求得AB答案可得.
解答 解:在△ACD中,∠DAC=30°,
∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1.
又∠BCD=180-60°-60°=60°,
故CB是△CAD底边AD的中垂线,
所以BD=BA、
在△ABC中,AB=$\frac{ACsin60°}{sin15°}$=$\frac{3\sqrt{2}+\sqrt{6}}{20}$,
因此,BD=$\frac{3\sqrt{2}+\sqrt{6}}{20}$≈0.3km.
故B、D的距离约为0.3km.
点评 本题主要考查了解三角形的实际应用.考查学生分析问题解决问题的能力.综合运用基础知识的能力.

练习册系列答案
相关题目
5.已知点P(x,y)满足x2+y2<2,则满足到直线x-y+2$\sqrt{2}$=0的距离d∈[1,3]的点P概率为( )
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $\frac{1}{2}-\frac{π}{2}$ | C. | $\frac{1}{4}-\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
6.集合{x∈N|x≤3}还可以表示为( )
| A. | {0,1,2,3} | B. | {2,1,3} | C. | {1,2,3,4} | D. | {x|0≤x≤3} |
3.设集合M={x|x>1},P={x|x2-6x+9=0},则下列关系中正确的是( )
| A. | M=P | B. | P?M | C. | M?P | D. | M∪P=R |
7.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=4x-1,则f(log4$\frac{1}{32}$)( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
4.方程(a-1)x2+(2-a)y2=(a-1)(2-a)中,当1<a<2时,它表示( )
| A. | 椭圆或圆 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |