题目内容
10.已知等比数列{an}的前n项和为Sn,且${a_3}=\frac{3}{2}$,${S_3}=\frac{9}{2}$.(1)若a3,m,S3成等比数列,求m值;
(2)求a1的值.
分析 (1)由a3,m,S3成等比数列,得m2=a3•S3,由此能求出m的值.
(2)设等比数列{an}公比为q,由q=1和q≠1两种情况分类讨论,能求出首项.
解答 解:(1)因为a3,m,S3成等比数列,所以 m2=a3•S3…(1分)
因为${a_3}=\frac{3}{2}$,${S_3}=\frac{9}{2}$,所以 ${m^2}=\frac{27}{4}$…(2分)
所以$m=±\frac{{3\sqrt{3}}}{2}$…(4分)
(2)设等比数列{an}公比为q,
①当q=1时,${a_1}={a_2}={a_3}=\frac{3}{2}$,此时${S_3}=\frac{9}{2}$,满足题意,…(6分)
②当q≠1时,依题意得$\left\{\begin{array}{l}{a_1}{q^2}=\frac{3}{2}\\ \frac{{{a_1}(1-{q^3})}}{1-q}=\frac{9}{2}\end{array}\right.$…(8分)
解得$\left\{\begin{array}{l}{a_1}=6\\ q=\frac{1}{2}\end{array}\right.$,综上可得${a_1}=\frac{3}{2}$或a1=6.…(12分)
点评 本题考查实数值的求法,考查数列的首项的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
5.某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,下表是这24套住宅每平方米的销售价格:(单位:万元/平方米):
(Ⅰ)这24套住宅中,求一套B户型住宅总价格超过任意一套A户型住宅总价格的概率;
(Ⅱ)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会.
小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格.为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
| 房41017 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.3 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.3 | 4.4 | 4.1 | 4.2 | 4.3 | 4.5 |
(Ⅱ)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会.
小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格.为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
19.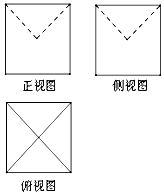 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
2.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}}$+4x的值域为( )
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
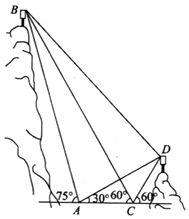 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.