题目内容
20．已知向量$\overrightarrow a=（1，2），\overrightarrow b=（1，0），\overrightarrow c=（3，-4）$，若λ为实数且$（\overrightarrow a+λ\overrightarrow b）$∥$\overrightarrow c$，则λ=$-\frac{5}{2}$．分析 求出共线的向量，利用向量共线的充要条件，列出方程求解即可．
解答 解：向量$\overrightarrow a=（1，2），\overrightarrow b=（1，0），\overrightarrow c=（3，-4）$，
$（\overrightarrow a+λ\overrightarrow b）$=（1+λ，2）．
λ为实数且$（\overrightarrow a+λ\overrightarrow b）$∥$\overrightarrow c$，
可得：-4-4λ=6，解得λ=-$\frac{5}{2}$．
故答案为：-$\frac{5}{2}$．
点评 本题考查向量共线的充要条件的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
8．在△ABC中，若c=2acosB，则△ABC的形状一定是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 等腰或直角三角形 | D． | 等腰三角形 |
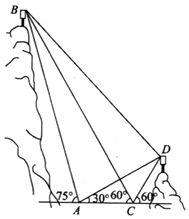如图，A，B，C，D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶．测量船于水面A处测得B点和D点的仰角分别为75°，30°，于水面C处测得B点和D点的仰角均为60°，AC=1km．试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D间的距离．（计算结果精确到0.1km）参考数据：$\sqrt{2}≈1.41$，$\sqrt{6}$≈2.45．
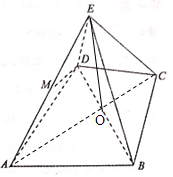如图几何体E-ABCD是四棱锥，△ABD为正三角形，∠BCD=120°，CB=CD=CE=1，AB=AD=AE=$\sqrt{3}$，且EC⊥BD，
12．已知函数f（x）=lnx+$\frac{1}{2}$ax2-2x有两个极值点，则a的取值范围是（ ）
| A． | （-∞，1） | B． | （0，2） | C． | （0，1） | D． | （0，3） |
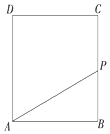如图所示，动点P从边长为1的正方形ABCD的顶点A出发，顺次经过顶点B，C，D再回到A．设x表示P点的路程，y表示PA的长度，求y关于x的函数关系式．