题目内容
7.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=4x-1,则f(log4$\frac{1}{32}$)( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 由已知得f(log4$\frac{1}{32}$)=f(-$\frac{5}{2}$)=f(-$\frac{1}{2}$)=-f($\frac{1}{2}$),由此能求出结果.
解答 解:∵f(x)是定义在R上周期为2的奇函数,
当x∈(0,1)时,f(x)=4x-1,
∴f(log4$\frac{1}{32}$)=f(-$\frac{5}{2}$)=f(-$\frac{1}{2}$)=-f($\frac{1}{2}$)=-(${4}^{\frac{1}{2}}$-1)=-1.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
12.已知函数f(x)=lnx+$\frac{1}{2}$ax2-2x有两个极值点,则a的取值范围是( )
| A. | (-∞,1) | B. | (0,2) | C. | (0,1) | D. | (0,3) |
19.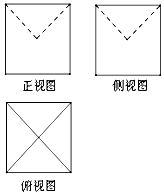 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
19.函数f(x)的导函数为f'(x),且满足f(x)=3x2+2xf'(2),则f'(5)的值为( )
| A. | 5 | B. | 1 | C. | 6 | D. | -2 |
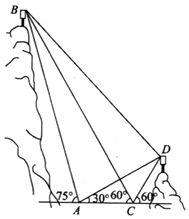 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.