题目内容
7.已知函数f(x)=(sinx+cosx)2+2cos2x(1)求f(x)的单调递减区间
(2)求f(x)在$x∈[0,\frac{π}{2}]$时的值域
(3)叙述由$y=\sqrt{2}sinx$到y=f(x)的图象的变换过程.
分析 首先画出三角函数式为最简形式,然后根据正弦函数的性质解之.
解答 解:由已知f(x)=(sinx+cosx)2+2cos2x=1+sin2x+cos2x+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2,
所以(1)令2x+$\frac{π}{4}$∈[2kπ+$\frac{π}{2}$,2kπ$+\frac{3π}{2}$],得到f(x)的单调递减区间为[k$π+\frac{π}{8}$,k$π+\frac{5π}{8}$],k∈Z;
(2)$x∈[0,\frac{π}{2}]$时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],所以f(x)的值域为[1,2+$\sqrt{2}$];
(3)由$y=\sqrt{2}sinx$的任何一点的横坐标缩小为原来的$\frac{1}{2}$,纵坐标不变,然后向左平移$\frac{π}{8}$个单位,最后向上平移2个单位得到y=f(x)的图象.
点评 不同考查了三角函数式的化简以及利用正弦函数的性质解答关于正弦型函数的性质.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
2.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}}$+4x的值域为( )
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
19.函数f(x)的导函数为f'(x),且满足f(x)=3x2+2xf'(2),则f'(5)的值为( )
| A. | 5 | B. | 1 | C. | 6 | D. | -2 |
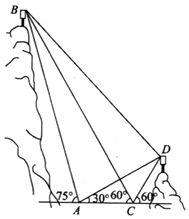 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:$\sqrt{2}≈1.41$,$\sqrt{6}$≈2.45.