题目内容
20.某工厂对一批共50件的机器零件进行分类检测,其重量(克)统计如下:| 重量段 | [80,85) | [85,90) | [90,95) | [95,100) |
| 件数 | 5 | m | 12 | n |
(1)从该批零件中任选1件,若选出的零件重量在[95,100]内的概率为0.26,求m的值;
(2)从重量在[80,85)的5件零件中,任选2件,求其中恰有1件为甲型的概率.
分析 (1)根据题设条件,先求出n的值,进而即可能求出m.
(2)重量在[80,85)的5件零件中,甲型2件,乙型3件,任选2件,先求出基本事件总数,再求出其中恰有1件为甲型包含的基本事件个数,由此能求出恰有1件为甲型的概率.
解答 解:(1)∵从该批零件中任选1件,选出的零件重量在[95,100]内的概率为0.26,
∴n=50×0.26=13,
∴m=50-5-12-13=20.
(2)∵重量在[80,85)的5件零件中,甲型2件,乙型3件,
从重量在[80,85)的5件零件中,任选2件,基本事件总数n=${C}_{5}^{2}$=10,
其中恰有1件为甲型包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,
∴其中恰有1件为甲型的概率p=$\frac{m}{n}$=0.6.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
15.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,x≥1}\\{1,x<1}\end{array}\right.$,则不等式f(6-x2)>f(x)的解集为( )
| A. | (-3,1) | B. | (-2,1) | C. | (-$\sqrt{5}$,2) | D. | (-2,$\sqrt{5}$) |
5.在用数学归纳法证明等式1+2+3+…+2n=2n2+n(n∈N*)的第(ii)步中,假设n=k时原等式成立,那么在n=k+1时需要证明的等式为( )
| A. | 1+2+3+…+2k+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| B. | 1+2+3+…+2k+2(k+1)=2(k+1)2+(k+1) | |
| C. | 1+2+3+…+2k+2k+1+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| D. | 1+2+3+…+2k+2k+1+2(k+1)=2(k+1)2+(k+1) |
9.设复数z满足(1+i)z=2i,其中i为虚数单位,则z的共轭复数$\overline{z}$=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
10.在伸缩变换$\left\{\begin{array}{l}{x′=3x}\\{y′=y}\end{array}\right.$的作用后,点(1,2)的坐标变为( )
| A. | (3,2) | B. | (1,2) | C. | ($\frac{1}{3}$,2) | D. | (1,$\frac{2}{3}$) |
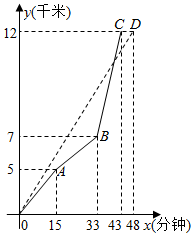 如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.
如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.