题目内容
15.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,x≥1}\\{1,x<1}\end{array}\right.$,则不等式f(6-x2)>f(x)的解集为( )| A. | (-3,1) | B. | (-2,1) | C. | (-$\sqrt{5}$,2) | D. | (-2,$\sqrt{5}$) |
分析 由题意y1=2x-1在[1,+∞)上单调递增,y2=1在(-∞,1)上是常数,利用f(6-x2)>f(x),可得6-x2>x≥1或2-x2>1且x<1,解不等式可求.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,x≥1}\\{1,x<1}\end{array}\right.$,y1=2x-1在[1,+∞)上单调递增,y2=1在(-∞,1)上是常数,
由分段函数的性质可知,
∵f(6-x2)>f(x)
∴6-x2>x≥1或6-x2>1且x<1,
解可得,1≤x<2或-$\sqrt{5}$<x<1,
即:x∈($-\sqrt{5}$,2)
故选:C.
点评 本题主要考查了利用分段函数的单调性求解不等式,解题的关键是确定函数的单调性.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.已知函数$f(x)=\left\{\begin{array}{l}\frac{2}{x},x>1\\ 9x{({1-x})^2},x≤1\end{array}\right.$,若函数g(x)=f(x)-k仅有一个零点,则k的取值范围是( )
| A. | $({\frac{4}{3},2}]$ | B. | $({-∞,0})∪({\frac{4}{3},+∞})$ | C. | (-∞,0) | D. | $({-∞,0})∪({\frac{4}{3},2})$ |
20.某工厂对一批共50件的机器零件进行分类检测,其重量(克)统计如下:
规定重量在82克及以下的为甲型,重量在85克及以上的为乙型,已知该批零件有甲型2件.
(1)从该批零件中任选1件,若选出的零件重量在[95,100]内的概率为0.26,求m的值;
(2)从重量在[80,85)的5件零件中,任选2件,求其中恰有1件为甲型的概率.
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100) |
| 件数 | 5 | m | 12 | n |
(1)从该批零件中任选1件,若选出的零件重量在[95,100]内的概率为0.26,求m的值;
(2)从重量在[80,85)的5件零件中,任选2件,求其中恰有1件为甲型的概率.
4.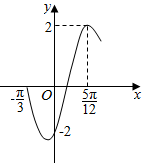 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )| A. | $2\;,\;-\frac{π}{3}$ | B. | $2\;,\;-\frac{π}{6}$ | C. | $4\;,\;-\frac{π}{6}$ | D. | $4\;,\;\frac{π}{3}$ |
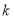 ,直线
,直线 与圆
与圆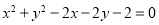 的位置关系是________
的位置关系是________