题目内容
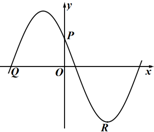 如图,点P(0,
如图,点P(0,| A |
| 2 |
| 2π |
| 9 |
| t | ||
|
(Ⅰ)求φ的值;
(Ⅱ)若PQ⊥PR,求A的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质,平面向量及应用
分析:(Ⅰ)由函数经过点P(0,
),得到sinφ=
,结合φ的范围求得φ的值;
(Ⅱ)由(Ⅰ)求出函数解析式,然后求出Q和R点的坐标,进一步求出
,
的坐标,然后由数量积等于0求得A的值.
| A |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)求出函数解析式,然后求出Q和R点的坐标,进一步求出
| PQ |
| PR |
解答:
解:(I)∵函数经过点P(0,
),∴sinφ=
,
又∵φ∈[0,2π),且点P在递减区间上,∴ϕ=
;
(II)由(I)可知y=Asin(
+
),令y=0,
得sin(
x+
)=0,∴
x+
=0,
∴x=-
,∴Q(-
,0).
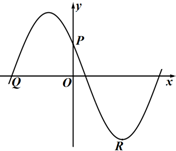
令y=-A,得sin(
x+
)=-1,
∴
x+
=
,
∴x=3,
∴R(3,-A).
又∵P(0,
),
∴
=(-
,-
),
=(3,-
),
∵PQ⊥PR,
∴
•
=-
+
A2=0,解得:A=
.
| A |
| 2 |
| 1 |
| 2 |
又∵φ∈[0,2π),且点P在递减区间上,∴ϕ=
| 5π |
| 6 |
(II)由(I)可知y=Asin(
| 2π |
| 9 |
| 5π |
| 6 |
得sin(
| 2π |
| 9 |
| 5π |
| 6 |
| 2π |
| 9 |
| 5π |
| 6 |
∴x=-
| 15 |
| 4 |
| 15 |
| 4 |

令y=-A,得sin(
| 2π |
| 9 |
| 5π |
| 6 |
∴
| 2π |
| 9 |
| 5π |
| 6 |
| 3π |
| 2 |
∴x=3,
∴R(3,-A).
又∵P(0,
| A |
| 2 |
∴
| PQ |
| 15 |
| 4 |
| A |
| 2 |
| PR |
| 3A |
| 2 |
∵PQ⊥PR,
∴
| PQ |
| PR |
| 45 |
| 4 |
| 3 |
| 4 |
| 15 |
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数的解析式,考查了平面向量的数量积,体现了数学转化思想方法,是中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
如表是一个2×2列联表,则表中a,b处的值分别为( )
| y1 | y2 | 总计 | |
| x1 | a | 21 | 73 |
| x2 | 8 | 25 | 33 |
| 总计 | b | 46 |
| A、94 96 |
| B、52 50 |
| C、52 60 |
| D、54 52 |
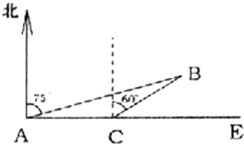 2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?
2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?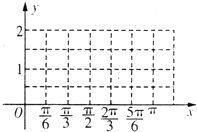 已知函数f(x)=sin(2ωx-
已知函数f(x)=sin(2ωx-