题目内容
3.复数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},x∈[-1.1]}\\{\frac{1}{x},x∈(1,+∞)}\end{array}\right.$,则$\int_0^2{f(x)}$dx=$\frac{π}{4}$+ln2.分析 利用定积分的可加性将所求写成两个定积分相加的形式,然后计算定积分.
解答 解:由已知${∫}_{0}^{1}\sqrt{1-{x}^{2}}dx+{∫}_{1}^{2}\frac{1}{x}dx$=$\frac{1}{4}π×{1}^{2}+lnx{|}_{1}^{2}$=$\frac{π}{4}$+ln2;
故答案为:$\frac{π}{4}+ln2$.
点评 本题考查了定积分的计算;利用定积分的运算法则将所求转化为两个定积分的和的形式是关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
14.定义A*B,B*A,C*D,D*A的运算分别对应图2中的(1)(2)(3)(4),那么,图1中(A)(B)可能是下列的运算的结果( )
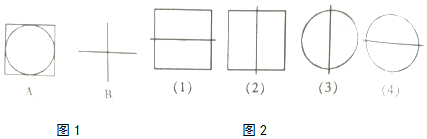

| A. | B*D,A*D | B. | B*D,A*C | C. | B*C,A*D | D. | C*D,A*D |
18.直线l过点(1,0)且与曲线y=-$\frac{1}{{e}^{x}}$相切,设其倾斜角为α,则α=( )
| A. | 30° | B. | 60° | C. | 45° | D. | 135° |
3.-3290°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |