题目内容
18.直线l过点(1,0)且与曲线y=-$\frac{1}{{e}^{x}}$相切,设其倾斜角为α,则α=( )| A. | 30° | B. | 60° | C. | 45° | D. | 135° |
分析 设出切点坐标,求出函数的导数,利用导数的几何意义求出切线的斜率,由点斜式求出切线方程,代入点(1,0),解方程即可得到结论.
解答 解:∵y=-$\frac{1}{{e}^{x}}$,
∴函数的导数为y′=$\frac{1}{{e}^{x}}$,
设切点坐标为(x0,-$\frac{1}{{e}^{{x}_{0}}}$),
∴切线方程为y+$\frac{1}{{e}^{{x}_{0}}}$=$\frac{1}{{e}^{{x}_{0}}}$(x-x0),
∵切线l过点(1,0),
∴$\frac{1}{{e}^{{x}_{0}}}$=$\frac{1}{{e}^{{x}_{0}}}$(1-x0),
解得x0=0,
∴$\frac{1}{{e}^{{x}_{0}}}$=1=tanα,
∴α=45°,
故选C.
点评 本题主要考查导数的几何意义,考查直线方程的形式,求函数的导数是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表数据:
根据最小二乘法建立的回归直线方程为$\widehaty=-20x+250$,
(1)试求表格中m的值;
(2)预计在今后的销售中,销量与单价仍然服从建立的回归方程,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | m | 75 | 68 |
(1)试求表格中m的值;
(2)预计在今后的销售中,销量与单价仍然服从建立的回归方程,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
10.已知非零向量$\overrightarrow{AB},\overrightarrow{AC}$满足$(\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|cosB}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|cosC}})•\overrightarrow{BC}=\overrightarrow{AB}•\overrightarrow{AC}$,则△ABC为( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
18.已知函数f(x)=x2+2x+a.若g(x)=$\frac{1}{{e}^{x}}$,对任意x1∈[$\frac{1}{2}$,2],存在x2∈[$\frac{1}{2}$,2],使f(x1)≤g(x2)成立,则实数a的取值范围是( )
| A. | (-∞,$\frac{\sqrt{e}}{e}$-8] | B. | [$\frac{\sqrt{e}}{e}$-8,+∞) | C. | [$\sqrt{2}$,e) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{e}{2}$] |
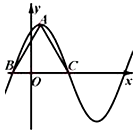 函数f(x)=6cos2$\frac{ωx}{2}$+2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.