题目内容
11.设函数f(x)=$\left\{\begin{array}{l}{1-|x-1|,x∈(-∞,2)}\\{\frac{1}{2}f(x-2),x∈[2,+∞)}\end{array}\right.$,则函数F(x)=xf(x)-1的零点的个数为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
分析 由F(x)=0得f(x)=$\frac{1}{x}$,然后分别作出函数f(x)与y=$\frac{1}{x}$的图象,利用数形结合即可得到函数零点的个数.
解答 解:由F(x)=xf(x)-1=0得,f(x)=$\frac{1}{x}$,然后分别作出函数f(x)与y=g(x)=$\frac{1}{x}$的图象如图:
∵当x≥2时,f(x)=$\frac{1}{2}$f(x-2),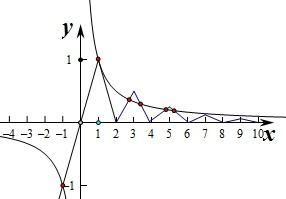
∴f(1)=1,g(1)=1,
f(3)=$\frac{1}{2}$f(1)=$\frac{1}{2}$,g(3)=$\frac{1}{3}$,
f(5)=$\frac{1}{2}$f(3)=$\frac{1}{4}$,g(5)=$\frac{1}{5}$,
f(7)=$\frac{1}{2}$f(5)=$\frac{1}{8}$,g(7)=$\frac{1}{7}$,
∴当x>7时,f(x)<$\frac{1}{x}$,
由图象可知两个图象的交点个数为6个.
故选:C.
点评 本题主要考查函数零点个数的判断,根据方程和函数之间的关系,转化为两个函数图象的交点问题是解决本题的关键,利用数形结合是解决本题的基本思想.本题难度较大,综合性较强.

练习册系列答案
相关题目
6.为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表数据:
根据最小二乘法建立的回归直线方程为$\widehaty=-20x+250$,
(1)试求表格中m的值;
(2)预计在今后的销售中,销量与单价仍然服从建立的回归方程,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | m | 75 | 68 |
(1)试求表格中m的值;
(2)预计在今后的销售中,销量与单价仍然服从建立的回归方程,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
16.函数y=cos(2x+φ)(-π≤φ≤π)的图象向右平移$\frac{π}{2}$个单位后与函数$y=sin(2x+\frac{π}{3})$的图象重合,此时φ=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $-\frac{π}{6}$ |
20.若sin(${\frac{π}{6}$-α})=$\frac{1}{3}$,则2cos2(${\frac{π}{6}$+$\frac{α}{2}$)-1等于( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | -$\frac{17}{81}$ |