题目内容
20.已知函数f(x)=|x-5|-|x-2|.(1)若?x∈R,使得f(x)≤m成立,求m的范围;
(2)求不等式x2-8x+15+f(x)≤0的解集.
分析 (1)通过讨论x的范围,求出f(x)的分段函数的形式,求出m的范围即可;
(2)通过讨论x的范围,求出不等式的解集即可.
解答 解:(1)$f(x)=|x-5|-|x-2|=\left\{\begin{array}{l}3,\;x≤2\\ 7-2x,2<x<5\\-3,x≥5.\end{array}\right.$,
当2<x<5时,-3<7-2x<3,
所以-3≤f(x)≤3,
∴m≥-3;
(2)不等式x2-8x+15+f(x)≤0,
即-f(x)≥x2-8x+15由(1)可知,
当x≤2时,-f(x)≥x2-8x+15的解集为空集;
当2<x<5时,-f(x)≥x2-8x+15,
即x2-10x+22≤0,∴$5-\sqrt{3}≤x<5$;
当x≥5时,-f(x)≥x2-8x+15,
即x2-8x+12≤0,∴5≤x≤6;
综上,原不等式的解集为$\left\{{x\left|{5-\sqrt{3}≤x≤6}\right.}\right\}$.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.已知等差数列{an}的前10项和为165,a4=12,则a7=( )
| A. | 14 | B. | 18 | C. | 21 | D. | 24 |
8.已知抛物线y2=2px的焦点为F,△ABC的三个顶点都在抛物线上,且A(1,2),$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AF}$,则BC边所在的直线方程为( )
| A. | 2x-y-2=0 | B. | 2x-y-1=0 | C. | 2x+y-6=0 | D. | 2x+y-3=0 |
5.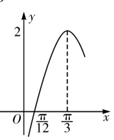 函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
 函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )| A. | [-$\sqrt{2}$,2] | B. | (-1,$\sqrt{2}$] | C. | [0,2] | D. | [-2,1] |
12.设Sn为正项等比数列{an}的前n项和,若a4•a8=2a10,则S3的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |