题目内容
5.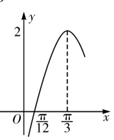 函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )| A. | [-$\sqrt{2}$,2] | B. | (-1,$\sqrt{2}$] | C. | [0,2] | D. | [-2,1] |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值可得f(x)的解析式;再根据y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式;再利用正弦函数的定义域和值域,求得g(x)在[0,$\frac{π}{6}$]上的取值范围.
解答 解:根据函数f(x)=Asin(ωx+θ)的图象,可得A=2,$\frac{1}{4}•\frac{2π}{ω}$=$\frac{π}{3}$-$\frac{π}{12}$,∴ω=2,
再根据五点法作图,可得2•$\frac{π}{12}$+φ=0,∴φ=-$\frac{π}{6}$,f(x)=2sin(2x-$\frac{π}{6}$).
将函数f(x)的图象向右平移$\frac{π}{6}$个单位,可得y=2sin(2x-$\frac{π}{3}$-$\frac{π}{6}$)=-2cos2x的图象;
再把纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,
得到函数g(x)=-2cos4x的图象.
在[0,$\frac{π}{6}$]上,4x∈[0,$\frac{2π}{3}$],cos4x∈[-$\frac{1}{2}$,1],∴g(x)=-2cos4x∈[-2,1],
故选:D.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值;y=Asin(ωx+φ)的图象变换规律;考查正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知a、b∈R,则“ab=1”是“直线“ax+y-l=0和直线x+by-1=0平行”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
16.为了研究学生的数学核素养与抽象(能力指标x)、推理(能力指标y)、建模(能力指标z)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标w=x+y+z的值评定学生的数学核心素养;若w≥7,则数学核心素养为一级;若5≤w≤6,则数学核心素养为二级;若3≤w≤4,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为a,从数学核心素养等级不是一级的学生中任取一人,其综合指标为b,记随机变量X=a-b,求随机变量X的分布列及其数学期望.
| 学生编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (2,2,3) | (3,2,3) | (3,3,3) | (1,2,2) | (2,3,2) | (2,3,3) | (2,2,2) | (2,3,3) | (2,1,1) | (2,2,2) |
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为a,从数学核心素养等级不是一级的学生中任取一人,其综合指标为b,记随机变量X=a-b,求随机变量X的分布列及其数学期望.
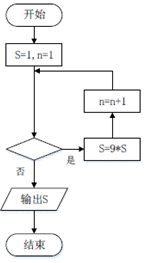 我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )
我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )