题目内容
20.已知函数f(x)=cos2x+2sinxcosx-sin2x,求:(1)函数f(x)的最小正周期;
(2)函数f(x)的单调递增区间.
分析 (1)由三角函数公式化简可得f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$),由周期公式可得;
(2)解2kπ+π≤2x-$\frac{π}{4}$≤2kπ+2π可得.
解答 解:(1)由三角函数公式化简可得f(x)=cos2x+2sinxcosx-sin2x
=cos2x-sin2x+2sinxcosx=cos2x+sin2x=$\sqrt{2}$cos(2x-$\frac{π}{4}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)由2kπ+π≤2x-$\frac{π}{4}$≤2kπ+2π可得kπ+$\frac{5π}{8}$≤x≤kπ+$\frac{9π}{8}$,
∴函数f(x)的单调递增区间为:[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$](k∈Z)
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和单调性,属基础题.

练习册系列答案
相关题目
11.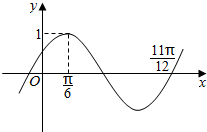 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )| A. | [2kπ-$\frac{π}{6}$,2kπ$+\frac{π}{3}$] | B. | [2k$π+\frac{π}{3}$,2kπ$+\frac{5π}{6}$] | C. | [kπ$+\frac{π}{3}$,kπ$+\frac{5π}{6}$] | D. | [kπ$-\frac{π}{6}$,kπ$+\frac{π}{3}$], |
15.设函数f(x)在点x0可导,且$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-2h)}{h}$=3,则f′(x0)=( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 3 |
5.已知函数y=f(x)的定义域为(0,+∞),当x>1时,f(x)<0,且对任意的x,y∈R,恒有f(xy)=f(x)+f(y),则不等式f(x)+f(x-2)≥f(8)的解集为( )
| A. | (2,4] | B. | [-2,4] | C. | [4,+∞) | D. | (-∞,-2]∪[4,+∞) |
10.已知a+a-1=2,则a-a-1的值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |
 如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.