题目内容
5.已知点F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1的直线l与双曲线C的左、右两支分别相交于点P,Q,若△PQF2是以∠Q为直角的等腰直角三角形,则双曲线C的离心率是$\sqrt{5+2\sqrt{2}}$.分析 可设|F1F2|=2c,|QF2|=m,若△PQF2是构成以Q为直角顶点的等腰直角三角形,则|PQ|=|QF2|=m,|PF2|=$\sqrt{2}$m,再由双曲线的定义,可得m,再由勾股定理,可得a,c的方程,运用离心率公式计算即可得到.
解答 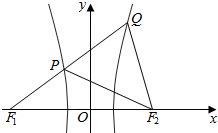 解:设|QF2|=m,Q在右支上,
解:设|QF2|=m,Q在右支上,
由双曲线的定义可得,|QF1|-|QF2|=2a,
∴|QF1|=2a+|QF2|=2a+m,
又|QF1|=|PQ|+|PF1|=m+|PF1|,
∴|PF1|=2a,又|PF2|-|PF1|=2a,
∴|PF2|=4a,
在等腰直角△PQF2中,|PF2|=$\sqrt{2}$m=4a,
解得m=2$\sqrt{2}$a,
在Rt△F1QF2中,|QF1|2+|QF2|2=4c2,
即(2a+2$\sqrt{2}$a)2+(2$\sqrt{2}$a)2=4c2,
即c2=(5+2$\sqrt{2}$)a2,
∴e=$\frac{c}{a}$=$\sqrt{5+2\sqrt{2}}$.
故答案为:$\sqrt{5+2\sqrt{2}}$.
点评 本题考查双曲线的定义、方程和性质,主要考查离心率的求法,同时考查勾股定理的运用,灵活运用双曲线的定义是解题的关键.

练习册系列答案
相关题目
15.设函数f(x)在点x0可导,且$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-2h)}{h}$=3,则f′(x0)=( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 3 |
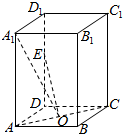 如图所示,在长方体体ABCD-A1B1C1D1中,O为AC的中点.
如图所示,在长方体体ABCD-A1B1C1D1中,O为AC的中点.