题目内容
7.计算:cos$\frac{4π}{3}$-tan(-$\frac{π}{4}$)+sin$\frac{3π}{2}$+(-2)°.分析 直接利用诱导公式以及特殊角的三角函数求解即可.
解答 解:cos$\frac{4π}{3}$-tan(-$\frac{π}{4}$)+sin$\frac{3π}{2}$+(-2)°
=-cos$\frac{π}{3}$+tan$\frac{π}{4}$+sin$\frac{3π}{2}$+1
=$-\frac{1}{2}$+1-1+1
=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查诱导公式的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,过F1作圆:x2+y2=$\frac{3}{4}$c2的切线,交双曲线左右支分别于A,B两点且|$\overrightarrow{BA}$|=|$\overrightarrow{B{F}_{2}}$|,则双曲线的离心率等于( )
| A. | $\sqrt{3}$+1 | B. | $\frac{\sqrt{15}+\sqrt{3}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{13}+1}{2}$ |
12.已知实数λ≠0,非零向量$\overrightarrow{a}$及零向量$\overrightarrow{0}$,下列各式不正确的是( )
| A. | $\overrightarrow{0}$•$\overrightarrow{a}$=$\overrightarrow{0}$ | B. | $\overrightarrow{a}$•$\overrightarrow{a}$=$\overrightarrow{a}$2 | C. | $\overrightarrow{a}$-$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | $\overrightarrow{a}$$+\overrightarrow{a}$=2$\overrightarrow{a}$ |
1.若平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{5}{12}$π | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
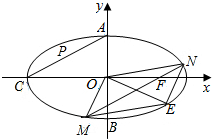 如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.
如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.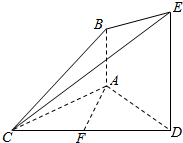 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.