题目内容
12.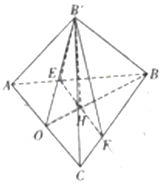 如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.
如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.(1)证明:B′H⊥平面ABC;
(2)求二面角B-B′A-C的余弦值.
分析 (1)证明EF⊥B′H,B′H⊥OH,即可得到B′H⊥平面ABC.
(2)以H为坐标原点,建立如图所示空间直角坐标系,求出法向量,利用向量法求解.
解答 解:(1)证明:∵△ABC是等腰三角形,
且AB=BC,又$AE=CF=\frac{5}{4}$,∴$\frac{BE}{EA}=\frac{BF}{FC}$,则EF∥AC.
又由AB=BC,得AC⊥BO,则EF⊥BO,
∴EF⊥BH,故H为EF中点,则EF⊥B′H,
∵AC=6,∴AO=3,
又AB=5,AO⊥OB,∴OB=4,
∴$OH=\frac{AE}{AB}\;•\;OB=1$,则BH=B′H=3,
∴|OB'|2=|OH|2+|B'H|2,则B′H⊥OH,
又OH∩EF=H,∴B′H⊥平面ABC.
(2)解:以H为坐标原点,建立如图所示空间直角坐标系,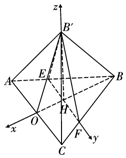
∵AB=5,AC=6,
∴B(-3,0,0),C(1,3,0),B'(0,0,3),A(1,-3,0),$\overrightarrow{AB}=(-4,\;\;3,\;\;0)$,$\overrightarrow{AB'}=(-1,\;\;3,\;\;3)$,$\overrightarrow{AC}=(0,\;\;6,\;\;0)$.
设平面ABB′的一个法向量为$\overrightarrow{n_1}=(x,\;\;y,\;\;z)$,
由$\left\{\begin{array}{l}\overrightarrow{n_1}\;•\;\overrightarrow{AB}=0,\;\;\\ \overrightarrow{n_1}\;•\;\overrightarrow{AB'}=0,\;\;\end{array}\right.$得$\left\{\begin{array}{l}-4x+3y=0,\;\;\\-x+3y+3z=0,\;\;\end{array}\right.$
取x=3,得y=4,z=-3.
∴$\overrightarrow{n_1}=(3,\;\;4,\;\;-3)$.
同理可求得平面AB′C的一个法向量$\overrightarrow{n_2}=(3,\;\;0,\;\;1)$.
设二面角B-B'A-C的平面角为θ,则$cosθ=\frac{{\overrightarrow{n_1}\;•\;\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}=\frac{3}{{\sqrt{85}}}$.
∴二面角B-B'A-C的余弦值为$cosθ=\frac{{3\sqrt{85}}}{85}$.
点评 本题考查了空间线面垂直的判定,向量法求解二面角,属于中档题.

| A. | -17 | B. | -15 | C. | -6 | D. | 0 |
| A. | $\frac{9}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{25}{36}$ | D. | 4 |
| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |