题目内容
设函数f(x)=
x2+bx-
.若对任意实数α,β,不等式f(cosα)≤0,f(2-sinβ)≥0恒成立,则b= .
| 1 |
| 4 |
| 3 |
| 4 |
考点:二次函数的性质
专题:函数的性质及应用
分析:结合三角函数的值域,及已知条件,可得f(x)=
x2+bx-
≤0在[-1,1]上恒成立且f(x)=
x2+bx-
≥0在[1,3]上恒成立,进而可得f(1)=0,进而得到答案.
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
解答:
解:∵cosα∈[-1,1],2-sinβ∈[1,3]
且f(cosα)≤0,f(2-sinβ)≥0恒成立,
故f(x)=
x2+bx-
≤0在[-1,1]上恒成立且f(x)=
x2+bx-
≥0在[1,3]上恒成立,
∴f(1)=
+b-
=0
故b=
,
故答案为:
且f(cosα)≤0,f(2-sinβ)≥0恒成立,
故f(x)=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
∴f(1)=
| 1 |
| 4 |
| 3 |
| 4 |
故b=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,其中根据已知分析出f(1)=0,是解答的关键.

练习册系列答案
相关题目
设集合A={x|0<x≤3},B={x|x<-1,或x>2},则A∩B=( )
| A、(2,3] |
| B、(-∞,-1)∪(0,+∞) |
| C、(-1,3] |
| D、(-∞,0)∪(2,+∞) |
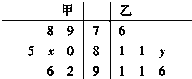 甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )
甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )