题目内容
已知函数f(x)=lg[(a2-1)x2+(a+1)x+1],设命题p:“f(x)的定义域为R”;命题q:“f(x)的值域是R”.
(1)若命题p为真,求实数a的取值范围;
(2)若命题p为假,命题q为真时,求实数a的取值范围.
(1)若命题p为真,求实数a的取值范围;
(2)若命题p为假,命题q为真时,求实数a的取值范围.
考点:复合命题的真假
专题:函数的性质及应用,简易逻辑
分析:(1)命题p为真,即f(x)的定义域为R,即(a2-1)x2+(a+1)x+1>0的解集为R,所以讨论a2-1=0,和a2-1≠0.a2-1=0时,容易得到a=-1时满足不等式解集为R,当a2-1≠0时,要使不等式的解集为R,则
,解该不等式并合并a=-1,便可得到a的取值范围;
(2)先求命题q为真时a的取值范围,要使f(x)的值域为R,则可设函数y=(a2-1)x2+(a+1)x+1的值域为B,则有(0,+∞)⊆B,对于a2-1=0的情况,容易判断a=-1满足(0,+∞)⊆B,而a2-1≠0时,需满足
,求出该不等式的解合并a=-1即得a的取值范围.
|
(2)先求命题q为真时a的取值范围,要使f(x)的值域为R,则可设函数y=(a2-1)x2+(a+1)x+1的值域为B,则有(0,+∞)⊆B,对于a2-1=0的情况,容易判断a=-1满足(0,+∞)⊆B,而a2-1≠0时,需满足
|
解答:
解:(1)f(x)的定义域为R,则(a2-1)x2+(a+1)x+1>0的解集为R;
∴若a2-1=0,a=±1,a=1时2x+1>0,该不等式的解集不为R,即a≠1;a=-1时,1>0,该不等式解集为R;
若a2-1≠0,则
,解得a<-1,或a>
;
∴实数a的取值范围是(-∞,-1]∪(
,+∞);
(2)若f(x)的值域是R,则设y=(a2-1)x2+(a+1)x+1的值域为B,则(0,+∞)⊆B;
若a2-1=0,a=±1,a=1时,y=2x+1,该函数的值域为R,满足(0,+∞)⊆R,a=-1时,y=1显然不满足(0,+∞)⊆B,即a≠-1;
若a2-1≠0,即a≠±1,要使(0,+∞)⊆B,则
,解得1<a≤
;
∴1≤a≤
;
∴实数a的取值范围是:[1,
].
∴若a2-1=0,a=±1,a=1时2x+1>0,该不等式的解集不为R,即a≠1;a=-1时,1>0,该不等式解集为R;
若a2-1≠0,则
|
| 5 |
| 3 |
∴实数a的取值范围是(-∞,-1]∪(
| 5 |
| 3 |
(2)若f(x)的值域是R,则设y=(a2-1)x2+(a+1)x+1的值域为B,则(0,+∞)⊆B;
若a2-1=0,a=±1,a=1时,y=2x+1,该函数的值域为R,满足(0,+∞)⊆R,a=-1时,y=1显然不满足(0,+∞)⊆B,即a≠-1;
若a2-1≠0,即a≠±1,要使(0,+∞)⊆B,则
|
| 5 |
| 3 |
∴1≤a≤
| 5 |
| 3 |
∴实数a的取值范围是:[1,
| 5 |
| 3 |
点评:考查一元二次不等式的解和判别式△的关系,二次函数值域的情况和判别式的关系,以及子集的概念.

练习册系列答案
相关题目
已知两点A(cosα,sinα)和B(cos2α,sin2α),则AB的长为( )
A、2sin
| ||
B、2|sin
| ||
C、2cos
| ||
D、2|cos
|
下列各图中,不可能表示函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
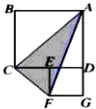 如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )
如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )| A、只与a的大小有关 |
| B、只与b的大小有关 |
| C、只与CE的大小有关 |
| D、无法确定 |
 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2切点分别为B,C.