题目内容
观察下列数据表,y与x之间的回归直线方程为 .
| x | -4 | -2 | 0 | 2 | 4 |
| y | -21 | -11 | 0 | 19 | 29 |
考点:线性回归方程
专题:计算题,概率与统计
分析:求出所给数据的平均数,得到样本中心点,根据线性回归直线过样本中心点,求出方程中的一个系数,得到线性回归方程.
解答:
解:
=
(-4-2+0+2+4)=0,
=
(-21-11+0+19+29)=3.2,
∴
=
=6.5,a=3.2-5•0=3.2.
∴y与x之间的回归直线方程为
=6.5x+3.2.
故答案为:
=6.5x+3.2.
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
∴
 |
| b |
| 84+22+38+116-5•0•3.2 |
| 16+4+4+16-5•02 |
∴y与x之间的回归直线方程为
 |
| y |
故答案为:
 |
| y |
点评:本题考查求回归方程,解题的关键是根据回归方程必过样本中心点,求出回归系数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x、y满足约束条件
,则目标函数z=2x+y( )
|
| A、最大值为1 |
| B、最大值为2 |
| C、最大值为3 |
| D、以上都不对 |
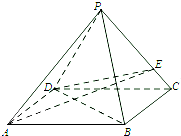 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2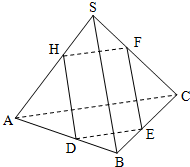 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于