题目内容
等差数列{an}的前n项和为Sn.已知a1=10,a2为整数,且Sn≤S4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=
,求数列{bn}的前n项和Tn.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| anan+1 |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由题意得a4≥0,a5≤0,即10+3d≥0,10+4d≤0,解得d=-3,即可写出通项公式;
(Ⅱ)利用裂项相消法求数列和即可.
(Ⅱ)利用裂项相消法求数列和即可.
解答:
解:(Ⅰ)由a1=10,a2为整数,且Sn≤S4得s3≤s4,s5≤s4,即s4-s3≥0,s5-s4≤0,
∴a4≥0,a5≤0,即10+3d≥0,10+4d≤0,解得-
≤d≤-
,
∴d=-3,
∴{an}的通项公式为an=13-3n.
(Ⅱ)∵bn=
=
(
-
),
∴Tn=b1+b2+…+bn=
(
-
+
-
+…+
-
)=
(
-
)=
.
∴a4≥0,a5≤0,即10+3d≥0,10+4d≤0,解得-
| 10 |
| 3 |
| 5 |
| 2 |
∴d=-3,
∴{an}的通项公式为an=13-3n.
(Ⅱ)∵bn=
| 1 |
| (13-3n)(10-3n) |
| 1 |
| 3 |
| 1 |
| 10-3n |
| 1 |
| 13-3n |
∴Tn=b1+b2+…+bn=
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 10 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 10-3n |
| 1 |
| 13-3n |
| 1 |
| 3 |
| 1 |
| 10-3n |
| 1 |
| 10 |
| n |
| 10(10-3n) |
点评:本题主要考查数列通项公式及数列和的求法,考查学生对裂项相消求和的能力及运算能力,属中档题.

练习册系列答案
相关题目
已知底面边长为1,侧棱长为
的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
已知
,
为单位向量,其夹角为60°,则(2
-
)•
=( )
| a |
| b |
| a |
| b |
| b |
| A、-1 | B、0 | C、1 | D、2 |
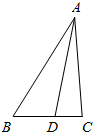 如图,在△ABC中,∠B=
如图,在△ABC中,∠B=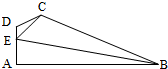 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=