题目内容
17.已知关于x的不等式|ax-2|+a|x-1|≥2(a>0).(1)当a=1时,求不等式的解集;
(2)若不等式的解集为R,求实数a的取值范围.
分析 (1)当a=1时,关于x的不等式即|x-2|+|x-1|≥2.而由绝对值的意义可得,$\frac{5}{2}$和$\frac{1}{2}$到1和2对应点的距离之和正好等于2,由此可得不等式的解集.
(2)由于|ax-2|+|ax-a|≥|a-2|,不等式的解集为R,等价于|a-2|≥2,由此求得a的范围.再根据a>0,进一步确定a的范围.
解答 解:(1)当a=1时,关于x的不等式|ax-2|+a|x-1|≥2(a>0),即|x-2|+|x-1|≥2.
而由绝对值的意义可得|x-2|+|x-1|表示数轴上的x对应点到1和2对应点的距离之和,
且$\frac{5}{2}$和$\frac{1}{2}$到1和2对应点的距离之和正好等于2,
故不等式的解集为{x|x≥$\frac{5}{2}$,或x≤$\frac{1}{2}$}.
(2)由于不等式|ax-2|+a|x-1|≥|(ax-2)-(ax-a)|=|a-2|,
不等式|ax-2|+a|x-1|≥2(a>0)的解集为R,等价于|a-2|≥2,
即 a-2≥2,或 a-2≤-2,解得 a≥4,或 a≤0.
再根据a>0,可得 a≥4,即a的范围为[4,+∞).
点评 本题主要考查绝对值的意义,绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
2.已知等差数列{an}中,Sn为其前n项和,S4=π(其中π为圆周率),a4=2a2,现从此数列的前30项中随机选取一个元素,则该元素的余弦值为负数的概率为( )
| A. | $\frac{7}{15}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{30}$ |
7.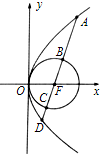 如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
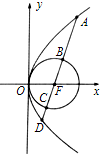 如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
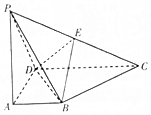 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.