Question

设实数x，y满足

(2x-y+2)(4x-y-2)≤0 0≤x≤2，y≥0

，若目标函数z=

m

n

x+y（m＞0，n＞0）的最大值为10，则2m+

1

n

的最小值为

 

．

Answer 1

考点：简单线性规划,基本不等式

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用目标函数的最大值确定最优解，利用基本不等式即可得到结论．

解答： 解：作出不等式组对应的平面区域，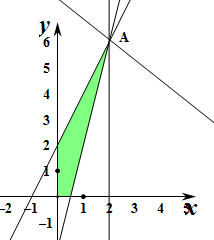
由z=

m

n

x+y（m＞0，n＞0），
得y=-

m

n

x+z（m＞0，n＞0），
则由图象可知当直线y=-

m

n

x+z经过点A时，截距最大，此时z最大为10，
由

2x-y+2=0 4x-y-2=0

，解得

x=2 y=6

，
即A（2，6），此时

2m

n

+6=10，
即m=2n，
∴2m+

1

n

=4n+

1

n

≥2

4n• 1 n

=4，
当且仅当4n=

1

n

，即n=

1

2

时取等号．
故答案为：4．

点评：本题主要考查线性规划的应用以及基本不等式的应用，利用数形结合是解决本题的关键．