题目内容
7.已知离心率为$\frac{\sqrt{2}}{2}$的椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)与圆N:x2+(y-1)2=$\frac{1}{2}$的公共弦长为$\sqrt{2}$(1)求椭圆C的方程;
(2)若椭圆C上存在两个不同的点A,B关于过点M(-$\frac{b}{2}$,0)且不与坐标轴垂直的直线l对称,O为坐标原点,求△AOB面积的最大值,求此时直线l的方程.
分析 (1)由题意结合对称性,可得椭圆经过点(±$\frac{\sqrt{2}}{2}$,1),代入椭圆方程,运用椭圆的离心率公式,解方程可得a,b,进而得到椭圆方程;
(2)设直线AB:y=kx+m(k≠0),由$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}+2{x}^{2}=2}\end{array}\right.$可得(2+k2)x2+2kmx+m2-2=0,运用韦达定理和中点坐标公式,以及弦长公式,以及点到直线的距离公式,运用三角形的面积公式,结合二次函数的最值求法,可得最小值及直线l的方程.
解答 解:(1)由椭圆和圆关于y轴对称,且公共弦长为$\sqrt{2}$,
可得椭圆经过点(±$\frac{\sqrt{2}}{2}$,1),
即有e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,$\frac{1}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1,
解得a=$\sqrt{2}$,b=1,
即有椭圆的方程为$\frac{{y}^{2}}{2}$+x2=1:
(2)设直线AB:y=kx+m(k≠0),
由$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}+2{x}^{2}=2}\end{array}\right.$可得(2+k2)x2+2kmx+m2-2=0,
由△>0可得m2-k2<2①
x1+x2=-$\frac{2km}{2+{k}^{2}}$,x1x2=$\frac{{m}^{2}-2}{2+{k}^{2}}$,
AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{km}{2+{k}^{2}}$,
纵坐标为k•(-$\frac{km}{2+{k}^{2}}$)+m=$\frac{2m}{2+{k}^{2}}$,
由k≠0,可得直线l的方程为y=-$\frac{1}{k}$(x+$\frac{1}{2}$),
将AB的中点坐标代入直线l,可得m=-$\frac{2+{k}^{2}}{2k}$,②
由①②可得k2>$\frac{2}{3}$,
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\frac{\sqrt{1+{k}^{2}}•\sqrt{3{k}^{4}+4{k}^{2}-4}}{|k|•(2+{k}^{2})}$,
原点到直线AB的距离为d=$\frac{2+{k}^{2}}{2\sqrt{1+{k}^{2}}•|k|}$,
即有S△AOB=$\frac{1}{2}$|AB|d=$\frac{\sqrt{2}•\sqrt{3{k}^{4}+4{k}^{2}-4}}{4{k}^{2}}$=$\frac{\sqrt{2}}{4}$•$\sqrt{-4(\frac{1}{{k}^{2}}-\frac{1}{2})^{2}+4}$,
由k2>$\frac{2}{3}$,可得k2=2即k=±$\sqrt{2}$时,S△AOB=取得最大值$\frac{\sqrt{2}}{2}$,
此时$\frac{1}{k}$=±$\frac{\sqrt{2}}{2}$,直线l的方程为y=±$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{4}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查三角形的面积的最值的求法,注意运用联立直线和椭圆方程,运用韦达定理和弦长公式、以及点到直线的距离公式,考查化简整理的运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 63 | B. | 66 | C. | 73 | D. | 76 |
| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{5}{3}x$ | C. | $y=±\frac{3}{5}x$ | D. | $y=±\sqrt{3}x$ |
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
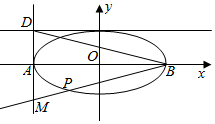 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.