题目内容
19.若$\frac{x}{{x}^{2}+x+1}=\frac{1}{5}$,求$\frac{{x}^{2}}{{x}^{4}{+x}^{2}+1}$的值.分析 由$\frac{x}{{x}^{2}+x+1}=\frac{1}{5}$得x2+x+1=5x,从而平方可得x4+2x2+1=16x2,从而解得.
解答 解:∵$\frac{x}{{x}^{2}+x+1}=\frac{1}{5}$,
∴x2+x+1=5x,
∴x2+1=4x,
∴x4+2x2+1=16x2,
即x4+x2+1=15x2,
故$\frac{{x}^{2}}{{x}^{4}{+x}^{2}+1}$=$\frac{1}{15}$.
点评 本题考查了学生的化简运算能力及方程思想的应用.

练习册系列答案
相关题目
14.5名大学生为唐山世界园艺博览会的3个场馆提供翻译服务,每个场馆分配一名或两名大学生,则不同的分配方法有( )
| A. | 90种 | B. | 180种 | C. | 270种 | D. | 360种 |
6.某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见表.规定:A、B、C三级为合格等级,D为不合格等级.
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.

| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.

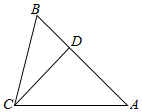 △ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.
△ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.