题目内容
12.已知向量$\overrightarrow{a}$=(k2,k+1),$\overrightarrow{b}$=(k,4),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数k值是0或$\frac{1}{3}$.分析 由向量平行可得k的方程,解方程可得.
解答 解:∵向量$\overrightarrow{a}$=(k2,k+1),$\overrightarrow{b}$=(k,4)且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴4k2=k(k+1),整理可得k(3k-1)=0,
解得k=0或k=$\frac{1}{3}$
故答案为:0或$\frac{1}{3}$
点评 本题考查平面向量的平行与共线,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知a>c>b>0,则对$\frac{a-b}{c}$+$\frac{b-c}{a}$+$\frac{c-a}{b}$的符号判断正确的是( )
| A. | 只取正号 | B. | 只取负号 | ||
| C. | 可取正号,也可取负号 | D. | 可取正号,负号,也可取零 |
1.已知实数x,y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{x+y-4≤0}\\{x≥1}\\{\;}\end{array}\right.$,则$\frac{xy}{{x}^{2}+{y}^{2}}$的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{91}{218}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{4}$ |
2.现有一枚质地均匀且表面分别标有1、2、3、4、5、6的正方体骰子,将这枚骰子先后抛掷两次,这两次出现的点数之和大于点数之积的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{11}{36}$ |
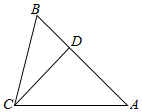 △ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.
△ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC. 某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.