题目内容
17.若点A$(\frac{π}{6},0)$、$B(\frac{π}{3},0)$是函数y=f(x)=sin(ωx+φ)的两个相邻零点,则$f(-\frac{π}{3})$=( )| A. | -1 | B. | 1 | C. | 0 | D. | $\frac{1}{2}$ |
分析 根据题意求出函数的周期与ω的值,再由点($\frac{π}{3}$,0)在函数f(x)图象上求出sinφ的值,从而求出f(-$\frac{π}{3}$)的值.
解答 解:点A$(\frac{π}{6},0)$、$B(\frac{π}{3},0)$是函数y=f(x)=sin(ωx+φ)的两个相邻零点,
∴T=$\frac{2π}{ω}$=2($\frac{π}{3}$-$\frac{π}{6}$)=$\frac{π}{3}$,
∴ω=6;
又点($\frac{π}{3}$,0)在函数f(x)图象上,
∴sin(6×$\frac{π}{3}$+φ)=sinφ=0,
∴f(-$\frac{π}{3}$)=sin[6×(-$\frac{π}{3}$)+φ]=sinφ=0.
故选:C.
点评 本题考查了函数y=Asin(ωx+φ)的图象与性质的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.运行如图所示的程序框图,输出的n等于( )
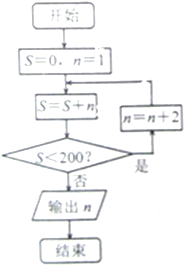

| A. | 30零 | B. | 29 | C. | 28 | D. | 27 |
5.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )


| A. | $\frac{1}{9}$ | B. | -1或1 | C. | -l | D. | l |
19.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)与g(x)=2cos(2x+φ)-1的图象有相同的对称轴,若$x∈[0,\frac{π}{2}]$,则f(x)的取值范围是( )
| A. | $(-\frac{3}{2},3)$ | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},\frac{3}{2}]$ | D. | [-3,3] |
20.执行如图所示的程序框图,则输出的n的值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
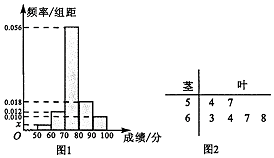 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.