题目内容
设数列{an}的前n项和为Sn,已知Sn=2an-2n+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:当x>0时,ln(x+1)>
;
(Ⅲ)令cn=(-1)n+1log
2,数列{cn}的前2n项和为T2n.利用(2)的结论证明:当n∈N*且n≥2时,
<ln2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:当x>0时,ln(x+1)>
| x |
| x+1 |
(Ⅲ)令cn=(-1)n+1log
| an |
| n+1 |
| T | 2n |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出an-2an-1=2n(n≥2),
-
=1,由此能求出数列{an}的通项公式.
(Ⅱ)令g(x)=ln(x+1)-
(x>0),利用导数求出g(x)>g(0)=0,从而能证明当x>0时,ln(x+1)>
.
(Ⅲ)由cn=(-1)n+1•
,知当n≥2时,T2n=1-
+
-
+…+
-
=
+
+…+
,由此能证明当n∈N*且n≥2时,
<ln2.
| an |
| 2n |
| an-1 |
| 2n-1 |
(Ⅱ)令g(x)=ln(x+1)-
| x |
| x+1 |
| x |
| x+1 |
(Ⅲ)由cn=(-1)n+1•
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| T | 2n |
解答:
(Ⅰ)解:由Sn=2an-2n+1,
得Sn-1=2an-1-2n(n≥2)…(2分)
两式相减,得an=2an-2an-1-2n,
即an-2an-1=2n(n≥2)
于是
-
=1,所以数列{
}是公差为1的等差数列…..….(3分)
又S1=2a1-22,所以a1=4.
所以
=2+(n-1)=n+1,
故an=(n+1)•2n.….(5分)
(Ⅱ)证明:令g(x)=ln(x+1)-
(x>0),
则g′(x)=
-
=
>0,(7分)
∴g(x)在(0,+∞)时单调递增,
g(x)>g(0)=0,
即当x>0时,ln(x+1)>
….(9分)
(Ⅲ)证明:因为cn=(-1)n+1•
,
所以当n≥2时,T2n=1-
+
-
+…+
-
=(1+
+
+…+
)-2(
+
+…+
)
=
+
+…+
.…(11分)
下面证
+
+…+
<ln2
令x=
,由(2)可得ln
>
,
所以ln(n+1)-lnn>
,ln(n+2)-ln(n+1)>
,…,ln(2n)-ln(2n-1)>
以上n个式相加,即有ln(2n)-lnn>
+
+…+
∴
+
+…+
<ln(2n)-lnn=ln2…(14分)
得Sn-1=2an-1-2n(n≥2)…(2分)
两式相减,得an=2an-2an-1-2n,
即an-2an-1=2n(n≥2)
于是
| an |
| 2n |
| an-1 |
| 2n-1 |
| an |
| 2n |
又S1=2a1-22,所以a1=4.
所以
| an |
| 2n |
故an=(n+1)•2n.….(5分)
(Ⅱ)证明:令g(x)=ln(x+1)-
| x |
| x+1 |
则g′(x)=
| 1 |
| x+1 |
| 1 |
| (x+1)2 |
| x |
| (x+1)2 |
∴g(x)在(0,+∞)时单调递增,
g(x)>g(0)=0,
即当x>0时,ln(x+1)>
| x |
| x+1 |
(Ⅲ)证明:因为cn=(-1)n+1•
| 1 |
| n |
所以当n≥2时,T2n=1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
=(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
下面证
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2n |
令x=
| 1 |
| n |
| n+1 |
| n |
| 1 |
| n+1 |
所以ln(n+1)-lnn>
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
以上n个式相加,即有ln(2n)-lnn>
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∴
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2n |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意导数性质和分组求和法的合理运用.

练习册系列答案
相关题目
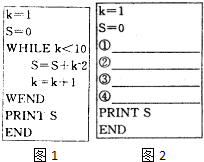 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: 为了测量一个心形图形的面积,现使用计算机设计一个模拟实验,将该图形放在一个边长为2cm的正方形中(如图所示),发现在正方形中的10000个随机的点中有3000个点落在该图形内,则这个心形图形的面积为
为了测量一个心形图形的面积,现使用计算机设计一个模拟实验,将该图形放在一个边长为2cm的正方形中(如图所示),发现在正方形中的10000个随机的点中有3000个点落在该图形内,则这个心形图形的面积为