Question

若实数a，b，c，d满足ab=2，c+2d=0，则（a-c）²+（b-d）²的最小值为

 

．

Answer 1

考点：基本不等式

专题：不等式的解法及应用

分析：分别画出函数y=

2

x

，y=-2x的图象，设直线y=-2x+t与曲线y=

2

x

相切于第一象限内的点P（m，n），则点P到直线y=-2x的距离即为所求．

解答： 解：分别画出函数y=

2

x

，y=-2x的图象，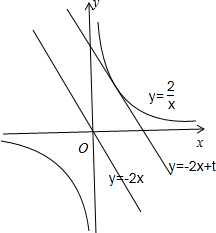
设直线y=-2x+t与曲线y=

2

x

相切于第一象限内的点P（m，n），
∵y′=-

2

x2

，∴-

2

m2

=-2，解得m=1，∴n=

2

1

=2．
∴切点为（1，2）．
由点到直线的距离公式可得d=

|2×1+2|

22+12

=

4 5

5

．
∴（a-c）²+（b-d）²的最小值为(

4 5

5

)2，化为

16

5

．
故答案为：

16

5

．

点评：本题考查了数形结合的思想方法、导数的几何意义、曲线的切线方程、转化方法等基础知识与基本技能方法，属于难题．