题目内容
7.定义一种新运算:$a?b=\left\{\begin{array}{l}b,(a≥b)\\ a,(a<b)\end{array}\right.$,已知函数$f(x)=\frac{4}{x}?(1+{log_2}x)(x>0)$,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为(0,2).分析 由新定义可得函数f(x)的解析式,问题等价于函数f(x)与y=k的图象有两个交点,作出函数的图象可得答案.
解答 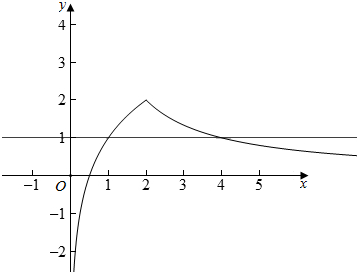 解:令$\frac{4}{x}$=1+log2x,可解得x=2,此时函数值为2,
解:令$\frac{4}{x}$=1+log2x,可解得x=2,此时函数值为2,
而且当0<x≤2时,$\frac{4}{x}$≥1+log2x,当x>2时$\frac{4}{x}$<1+log2x,
$f(x)=\frac{4}{x}?(1+{log_2}x)(x>0)$=$\left\{\begin{array}{l}{1+lo{g}_{2}x,0<x≤2}\\{\frac{4}{x},x>2}\end{array}\right.$,
函数g(x)=f(x)-k恰有两个零点等价于
函数f(x)与y=k的图象有两个交点,
作出函数的图象:
由图象可知,k的取值范围为(0,2),
故答案为:(0,2).
点评 本题考查根的存在性即个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
17.曲线$f(x)=\frac{1}{3}{x^3}-2$在点$({1,-\frac{5}{3}})$处的斜率为( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | -1 | D. | 1 |
18.已知幂函数y=f(x)的图象经过点$(4,\frac{1}{2})$,且f(a+1)<f(10-2a),则实数a的取值范围是( )
| A. | (-1,5) | B. | (-∞,3) | C. | (3,+∞) | D. | (3,5) |
2.某几何体的三视图如图所示,则该几何体的表面积为( )
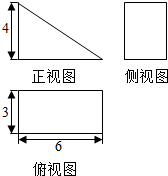

| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
19.设△ABC的内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:3:4,则cosC的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
16.已知某三棱锥的三视图尺寸(单位cm)如图,则这个三棱锥的体积是( )


| A. | $\frac{8}{3}c{m^3}$ | B. | $\frac{4}{3}c{m^3}$ | C. | $\frac{2}{3}c{m^3}$ | D. | $\frac{1}{3}c{m^3}$ |
17.方程$\sqrt{x}$-1nx-2=0的根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的众数为12.5.
如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的众数为12.5.