题目内容
2.某几何体的三视图如图所示,则该几何体的表面积为( )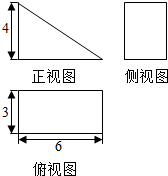
| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
分析 由已知中的三视图可得该几何体是一个以主视图为底面的三棱柱,代入柱体表面积公式,可得答案.
解答 解:由已知中的三视图可得该几何体是一个以主视图为底面的三棱柱,
底面面积为:$\frac{1}{2}$×4×6=12,
底面周长为:4+6+$\sqrt{{4}^{2}+{6}^{2}}$=10+2$\sqrt{13}$,
柱体的高为3,
故柱体的侧面积为:3×(10+2$\sqrt{13}$)=30+6$\sqrt{13}$,
故柱体的表面积S=2×12+30+6$\sqrt{13}$=54+6$\sqrt{13}$,
故选:B
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
13.在平面直角坐标系中,记不等式组$\left\{\begin{array}{l}{y-x≥0}\\{y-{x}^{2}≤0}\\{x≤2}\end{array}\right.$所围成的平面区域的面积为S,则S为( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | 1 |
17.已知集合P={0,1},Q={0},则( )
| A. | Q=∅ | B. | P=Q | C. | P?Q | D. | P⊆Q |
 某次运动会甲、乙两名射击运动员的成绩如下:
某次运动会甲、乙两名射击运动员的成绩如下: