题目内容
 已知定义在R上的函数f(x)满足f(2)=1,f′x)为f(x)的导函数.已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)>1,则
已知定义在R上的函数f(x)满足f(2)=1,f′x)为f(x)的导函数.已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)>1,则| b-1 |
| a-2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用,不等式的解法及应用
分析:先根据导函数的图象判断原函数的单调性,从而确定a、b的范围,最后利用线性规划的方法得到答案.
解答:
解:由图可知,当x>0时,导函数f'(x)<0,原函数单调递减,
∵两正数a,b满足f(2a+b)>1,且f(2)=1,
∴2a+b<2,a>0,b>0,画出可行域如图.
k=
的几何意义为点Q(2,1)与点P(x,y)连线的斜率,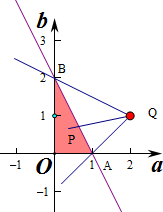
当P点在A(1,0)时,k最大,最大值为:
=1;
当P点在B(0,2)时,k最小,最小值为:
=-
.
k的取值范围是(-
,1).
故答案为:(-
,1).
∵两正数a,b满足f(2a+b)>1,且f(2)=1,
∴2a+b<2,a>0,b>0,画出可行域如图.
k=
| b-1 |
| a-2 |

当P点在A(1,0)时,k最大,最大值为:
| 1-0 |
| 2-1 |
当P点在B(0,2)时,k最小,最小值为:
| 1-2 |
| 2-0 |
| 1 |
| 2 |
k的取值范围是(-
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
点评:本题主要考查函数的单调性和导数之间的关系以及线性规划的应用,根据条件将不等式转化为线性规划问题是解决本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
实数x,y满足不等式组
,且z=x+y的最大值为9,则m=( )
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设f(x)是定义在实数集R上的函数,且满足下列关系f(10+x)=f(10-x),f(20-x)=-f(20+x),则f(x)是( )
| A、偶函数,但不是周期函数 |
| B、偶函数,又是周期函数 |
| C、奇函数,但不是周期函数 |
| D、奇函数,又是周期函数 |
 某种产品的成本f1(x)与年产量x之间的函数关系的图象是顶点在原点的抛物线的一部分(如图1),该产品的销售单价f2(x)与年销售量之间的函数关系图象(如图2),若生产出的产品都能在当年销售完.
某种产品的成本f1(x)与年产量x之间的函数关系的图象是顶点在原点的抛物线的一部分(如图1),该产品的销售单价f2(x)与年销售量之间的函数关系图象(如图2),若生产出的产品都能在当年销售完.