题目内容
实数x，y满足不等式组
，且z=x+y的最大值为9，则m=（ ）
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．
解答：
解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=x+y得y=-x+z，平移直线y=-x+z，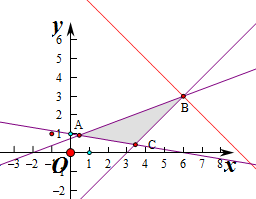
∵z=x+y的最大值为9，
∴平面区域在直线x+y=9的下方，
由图象可知当直线y=-x+z经过点B时，直线y=-x+z的截距最大，
此时z最大．
由
得
，即B（6，3），
同时B也在直线x-2my+2=0上，
代入得6-6m+2=0，
解得m=
，
故选：C
由z=x+y得y=-x+z，平移直线y=-x+z，
∵z=x+y的最大值为9，
∴平面区域在直线x+y=9的下方，
由图象可知当直线y=-x+z经过点B时，直线y=-x+z的截距最大，
此时z最大．
由
|
|
同时B也在直线x-2my+2=0上，
代入得6-6m+2=0，
解得m=
| 4 |
| 3 |
故选：C
点评：本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．利用平移确定目标函数取得最优解的条件是解决本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
若a＜b＜0，则下列不等关系中，不能成立的是（ ）
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|
下列命题中的假命题是（ ）
| A、?x∈R，2x-1＞0 |
| B、?x∈R，tanx=2 |
| C、?x∈R，lgx＜1 |
| D、?x∈N*，（x-1）2＞0 |
在R上定义运算?：x?y=x（1-y）若对任意x＞2，不等式（x-a）?x≤a-2都成立，则实数a的取值范围是（ ）
| A、（-∞，3） |
| B、（-∞，3] |
| C、（3，+∞） |
| D、[3，+∞） |
已知定义在R上的函数f（x）满足f（2）=1，f′x）为f（x）的导函数．已知y=f′（x）的图象如图所示，若两个正数a，b满足f（2a+b）＞1，则设函数f（x）是定义在（-∞，0）上的可导函数，起到函数为f′（x），且有xf′（x）＞x2+2f（x），则不等式4f（x+2015）-（x+2015）2f（-2）＞0的解集为（ ）
| A、（-∞，2017） |
| B、（-2017，0） |
| C、（-∞，-2016） |
| D、（-2016，0） |