题目内容
16.已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(-∞,0)时,xf'(x)<f(-x)(其中f'(x)是f(x)的导函数),若a=$\sqrt{3}$f($\sqrt{3})$,b=(lg3)f(lg3),c=$({log_3}\frac{1}{3})f({log_3}\frac{1}{3})$,则( )| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | a>c>b |
分析 设F(x)=xf(x),根据题意得F(x)是偶函数且在区间(0,+∞)上是增函数,由此比较$\sqrt{3}$、lg3和1的大小,结合函数的性质,不难得到本题的答案.
解答 解:设F(x)=xf(x),得F'(x)=x'f(x)+xf'(x)=xf'(x)+f(x),
∵当x∈(-∞,0)时,xf′(x)<f(-x),且f(-x)=-f(x)
∴当x∈(-∞,0)时,xf′(x)+f(x)<0,即F'(x)<0
由此可得F(x)=xf(x)在区间(-∞,0)上是减函数,
∵函数y=f(x)是定义在实数集R上的奇函数,
∴F(x)=xf(x)是定义在实数集R上的偶函数,在区间(0,+∞)上F(x)=xf(x)是增函数.
∵0<lg3<lg10=1,$\sqrt{3}$∈(1,2)
∴F(2)>F($\sqrt{3}$)>F(lg3)
∵log3$\frac{1}{3}$=-1,从而F(log3$\frac{1}{3}$)=F(-1)=F(1)
∴F($\sqrt{3}$)>F(log3$\frac{1}{3}$)>F(lg3)
得a>c>b,
故答案为:D
点评 本题给出抽象函数,比较几个函数值的大小.着重考查了利用导数研究函数的单调性、不等式比较大小和函数单调性与奇偶性关系等知识,属于中档题.

练习册系列答案
相关题目
11.如果函数f(x)=3cos(2x+$\frac{π}{6}$),则f(x)的图象( )
| A. | 关于点(-$\frac{π}{12}$,0)对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{2}$对称 |
8.如图是正方体的侧面展开图,l1、l2是两条侧面对角线,则在此正方体中,l1与l2( )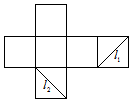

| A. | 互相平行 | B. | 相交且夹角为$\frac{π}{3}$ | C. | 异面且互相垂直 | D. | 异面且夹角为$\frac{π}{3}$ |
5.已知f(x)=4x5+3x4+2x3-x2-x-$\frac{1}{2}$,用秦九韶算法求f(-2)等于( )
| A. | -$\frac{197}{2}$ | B. | $\frac{197}{2}$ | C. | $\frac{183}{2}$ | D. | -$\frac{183}{2}$ |
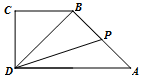 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.