题目内容
14.数列{an}满足a1=1,且an+1=a1+an+n(n∈N*),则$\frac{1}{a_1}+\frac{1}{a_2}+$…$+\frac{1}{{{a_{2016}}}}$等于( )| A. | $\frac{4032}{2017}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2014}{2015}$ |
分析 an+1=a1+an+n(n∈N*),a1=1.可得an+1-an=n+1,利用“累加求和”方法可得an=$\frac{n(n+1)}{2}$.可得$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.即可得出.
解答 解:∵an+1=a1+an+n(n∈N*),a1=1.
∴an+1-an=n+1,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+…+2+1=$\frac{n(n+1)}{2}$.
∴$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
则$\frac{1}{a_1}+\frac{1}{a_2}+$…$+\frac{1}{{{a_{2016}}}}$=$2[(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2016}-\frac{1}{2017})]$
=2$(1-\frac{1}{2017})$=$\frac{4032}{2017}$.
故选:A.
点评 本题考查了等差数列的通项公式与求和公式、“累加求和”方法与“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知集合A={x|x2-2x<0},B={y|y=|x|+1,x∈R},则A∩∁RB=( )
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
9.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
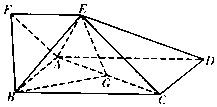 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.