题目内容
已知向量
=(f(x),1),向量
=(2x+|x|-1,2|x|),且满足
∥
(1)若f(x)=
,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[2,4]恒成立,求实数m的取值范围.
(3)若2tf(2t)+mf(t)≥0对于t∈[1,2]有解,求实数m的取值范围.
| a |
| b |
| a |
| b |
(1)若f(x)=
| 15 |
| 4 |
(2)若2tf(2t)+mf(t)≥0对于t∈[2,4]恒成立,求实数m的取值范围.
(3)若2tf(2t)+mf(t)≥0对于t∈[1,2]有解,求实数m的取值范围.
考点:导数在最大值、最小值问题中的应用,平行向量与共线向量
专题:综合题,不等式的解法及应用
分析:(1)由
∥
,得f(x)•2|x|=2x+|x|-1,由此可求f(x),然后解方程f(x)=
可得2x,进而得x;
(2)2tf(2t)+mf(t)≥0可化为2t(2t+2-t)+m≥0,从而化为[2t(2t+2-t)+m]min≥0,利用函数单调性易求最小值;
(3)由(2)可知不等式可转化为[2t(2t+2-t)+m]max≥0,利用单调性可求最大值;
| a |
| b |
| 15 |
| 4 |
(2)2tf(2t)+mf(t)≥0可化为2t(2t+2-t)+m≥0,从而化为[2t(2t+2-t)+m]min≥0,利用函数单调性易求最小值;
(3)由(2)可知不等式可转化为[2t(2t+2-t)+m]max≥0,利用单调性可求最大值;
解答:
解:(1)由
∥
,得f(x)•2|x|=2x+|x|-1,
∴f(x)=2x-2-|x|,
∵f(x)=
,∴2x-2-|x|=
,
可知x>0,∴2x-2-x=
,
解得2x=4,∴x=2.
(2)2tf(2t)+mf(t)≥0,即2t(22t-2-|2t|)+m(2t-2-|t|)≥0,
又t∈[2,4],
∴2t(22t-2-2t)+m(2t-2-t)≥0,即2t(2t+2-t)+m≥0,
而2t(2t+2-t)+m=22t+1+m≥22×2+1+m=17+m,
∴17+m≥0,解得m≥-17.
(3)由(2)知,2tf(2t)+mf(t)≥0对于t∈[1,2]有解,即2t(2t+2-t)+m≥0有解,
当t∈[1,2]时,2t(2t+2-t)+m=22t+1+m∈[5+m,17+m],
∴17+m≥0,解得m≥-17.
| a |
| b |
∴f(x)=2x-2-|x|,
∵f(x)=
| 15 |
| 4 |
| 15 |
| 4 |
可知x>0,∴2x-2-x=
| 15 |
| 4 |
解得2x=4,∴x=2.
(2)2tf(2t)+mf(t)≥0,即2t(22t-2-|2t|)+m(2t-2-|t|)≥0,
又t∈[2,4],
∴2t(22t-2-2t)+m(2t-2-t)≥0,即2t(2t+2-t)+m≥0,
而2t(2t+2-t)+m=22t+1+m≥22×2+1+m=17+m,
∴17+m≥0,解得m≥-17.
(3)由(2)知,2tf(2t)+mf(t)≥0对于t∈[1,2]有解,即2t(2t+2-t)+m≥0有解,
当t∈[1,2]时,2t(2t+2-t)+m=22t+1+m∈[5+m,17+m],
∴17+m≥0,解得m≥-17.
点评:该题考查函数恒成立、指数函数的单调性、向量共线的充要条件等知识,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
相关题目
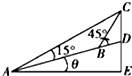 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100米到达B处,又测得C对于山坡的斜度为45°,若CD=50米,山坡对于地平面的坡角为θ,则cosθ=( )
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100米到达B处,又测得C对于山坡的斜度为45°,若CD=50米,山坡对于地平面的坡角为θ,则cosθ=( )A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
函数f(x)=lnx-x+2的零点所在的区间为( )
| A、(4,5) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |