题目内容
若
<
<0,则下列不等式:①|a|>|b|;②a+b>ab;③
+
>2;④
<2a-b中,正确的不等式是( )
| 1 |
| a |
| 1 |
| b |
| a |
| b |
| b |
| a |
| a2 |
| b |
| A、①② | B、③④ | C、①③ | D、②④ |
考点:基本不等式
专题:不等式的解法及应用
分析:取a=-1,b=-2,可得①②均错误,可得答案.
解答:
解:不妨取a=-1,b=-2,显然满足
<
<0,
可得①|a|>|b|错误;可排除选项A、C;
也可得②a+b>ab错误,可排除选项D,
故选:B.
| 1 |
| a |
| 1 |
| b |
可得①|a|>|b|错误;可排除选项A、C;
也可得②a+b>ab错误,可排除选项D,
故选:B.
点评:本题考查不等式比较大小,反例法是解决问题的关键,属基础题.

练习册系列答案
相关题目
函数f(x)=
-cosx在(0,+∞)内图象与X轴交点个数( )
| x |
| A、零个 | B、有且仅有一个 |
| C、有且仅有两个 | D、有无穷多个 |
在等差数列{an}中,已知a3+a8=9,则3a5+a7=( )
| A、10 | B、18 | C、20 | D、28 |
若ξ服从正态分布N(10,σ2),若P(ξ<11)=0.9,则P(|ξ-10|<1)=( )
| A、0.1 | B、0.2 |
| C、0.4 | D、0.8 |
某学校从1208名学生中抽取20人参加义务劳动,规定采用下列方式选取:先用简单随机抽样的方法从1208人中剔除8人,剩下的1200人再按系统抽样的方法抽取,那么在1208人中每个人入选的概率为( )
A、都相等且等于
| ||
B、都相等且等于
| ||
| C、不全相等 | ||
| D、均不相等 |
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.若sinC+sin(B-A)=sin2A,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
在一次试验中,所抽取的样本共有5个个体,其值分别为0,1,2,3,a.若该样本的平均值为1,则样本的标准差为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
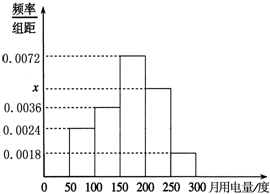 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )