题目内容
7.函数y=3sin(-2x-$\frac{π}{6}$)的单调递增区间( )| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) |
分析 化简函数y,根据三角函数的图象与性质即可求出函数y的单调递增区间.
解答 解:函数y=3sin(-2x-$\frac{π}{6}$)=-3sin(2x+$\frac{π}{6}$),
令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,k∈Z;
解得$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ,k∈Z;
∴函数y的单调递增区间为:
[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
故选:D.
点评 本题考查了三角函数的图象与性质的应用问题,属于基础题.

练习册系列答案
相关题目
12.若$P(-2,-\frac{π}{3})$是极坐标系中的一点,则$Q(2,\frac{2π}{3}),R(2,\frac{8π}{3})$,$M(-2,\frac{5π}{3})$$N(2,2kπ-\frac{5π}{3})$(k∈Z)四点中与P重合的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.在一个口袋中装5个白球和3个黑球,这些球除颜色外完全相同,从中摸出1个球,则摸到黑球的概率是( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
16.不等式组$\left\{\begin{array}{l}x>m\\ x<4\end{array}\right.$的整数解有4个,则m的取值范围是( )
| A. | -1≤m<0 | B. | -1<m≤0 | C. | -1≤m≤0 | D. | -1<m<0 |
17.若命题p:{x|log2(x-1)<0}命题 q:{x|x<3},则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
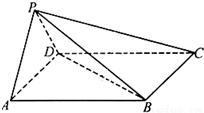 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.