题目内容
设集合A是函数f(x)=
+lg(2-x)的定义域,集合B是函数g(x)=2x的值域.
(1)求集合A∩B;
(2)设集合C={x|x<a},若集合A∩C=A,求实数a的取值范围.
| x+1 |
(1)求集合A∩B;
(2)设集合C={x|x<a},若集合A∩C=A,求实数a的取值范围.
考点:集合的包含关系判断及应用,交集及其运算
专题:集合
分析:(1)首先,确定集合A、B的元素组成,然后,求解集合A∩B;
(2)结合条件A∩C=A,得到A⊆C,然后,借助于子集的概念进行求解.
(2)结合条件A∩C=A,得到A⊆C,然后,借助于子集的概念进行求解.
解答:
解:(1)由集合A得:
,
∴-1≤x<2,
∴A={x|-1≤x<2},
由于集合B是函数g(x)=2x的值域,由指数函数的图象与性质,得B={y|y>0},
∴A∩B={x|0<x<2},
(2)∵A∩C=A,
∴A⊆C,
∴a≥2,
∴实数a的取值范围[2,+∞).
|
∴-1≤x<2,
∴A={x|-1≤x<2},
由于集合B是函数g(x)=2x的值域,由指数函数的图象与性质,得B={y|y>0},
∴A∩B={x|0<x<2},
(2)∵A∩C=A,
∴A⊆C,
∴a≥2,
∴实数a的取值范围[2,+∞).
点评:本题综合考查了集合之间的关系,集合的元素特征,函数的定义域和值域等知识,属于中档题.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知a>0且a≠1,则在下面所给出的四种图形中,正确表示函数y=ax和y=logax的图象一定是( )

| A、①③ | B、②③ | C、②④ | D、①④ |
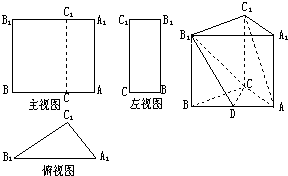 已知三棱柱ABC-A1B1C1的三视图与直观图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,B1C1=4,
已知三棱柱ABC-A1B1C1的三视图与直观图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,B1C1=4,