题目内容
李明所在的高二(16)班有58名学生,学校要从该班抽出5人开座谈会,若采用系统抽样法,需先剔除3人,再将留下的55人平均分成5个组,每组各抽一人,则李明参加座谈会的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:系统抽样的方法是一个等可能的抽样,故每个个体被抽到的概率都是相等的,由等可能事件的概率算出每个个体参加座谈会的概率即可
解答:
解:由题意58名学生,学校要从该班抽出5人开座谈会,故每个人被抽到的概率是
,
故李明参加座谈会的概率为
;
故选:C
| 5 |
| 58 |
故李明参加座谈会的概率为
| 5 |
| 58 |
故选:C
点评:本题考查系统抽样的方法,解题的关键是理解系统抽样是一个等可能抽样,即每个个体被抽到的概率相等,由此算出李明参加座谈会的概率.

练习册系列答案
相关题目
定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在,且满足
<x,则下列不等式成立的是( )
| f(x) |
| f′(x) |
| A、3f(2)<2f(3) |
| B、3f(4)<4f(3) |
| C、2f(3)<3f(4) |
| D、以上结论都不对 |
复数z满足z(2+i)=2i-1,则复数z的实部与虚部之和为( )
| A、1 | B、-1 | C、2 | D、3 |
已知实数x,y满足ax<ay(a>1),则下列关系式恒成立的是( )
A、
| ||||
| B、ln(x2+1)<ln(y2+1) | ||||
| C、sinx<siny | ||||
| D、x3<y3 |
在数列{an}中,a1=1,an+2+(-1)nan=2,记Sn为数列{an}的前项和,则S61=( )
| A、931 | B、961 |
| C、991 | D、1021 |
经过两直线x+3y-10=0和3x-y=0的交点,且和原点相距为1的直线的条数为( )
| A、0 | B、1 | C、2 | D、3 |
圆心在直线l:x-y+1=0上,且过A(1,1),B(2,-2)两点的圆的方程为( )
| A、(x-3)2+(y-2)2=25 |
| B、(x+3)2+(y-2)2=25 |
| C、(x-3)2+(y+2)2=25 |
| D、(x+3)2+(y+2)2=25 |
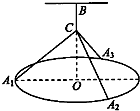 如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).
如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).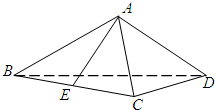 如图,在体积为
如图,在体积为