题目内容
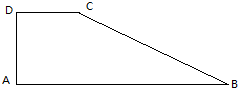如图，一直角梯形ABCD的上，上下底分别为CD=| 3 |
| 3 |
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：由题设∠ABC=30°，BC=4，分别过A、D作AM⊥BC，DN⊥BC垂足为M，N，则AM=
，DN=
，所求旋转体的表面积由三部分构成．
3
| ||
| 2 |
| ||
| 2 |
解答：
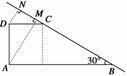解：由题设∠ABC=30°，BC=4，分别过A、D作AM⊥BC，DN⊥BC垂足为M，N，
则AM=
，DN=
，所求旋转体的表面积由三部分构成
①圆锥B-AM的侧面积S1=π•AM•AB=
π．
②圆台MN的侧面积S2=π（AM+DN）•AD=4
π．
③圆锥C-DN的侧面积S3=π•DN•CD=
π．
∴S表=S1+S2+S3=（15+4
）π．
解：由题设∠ABC=30°，BC=4，分别过A、D作AM⊥BC，DN⊥BC垂足为M，N，则AM=
3
| ||
| 2 |
| ||
| 2 |
①圆锥B-AM的侧面积S1=π•AM•AB=
| 27 |
| 2 |
②圆台MN的侧面积S2=π（AM+DN）•AD=4
| 3 |
③圆锥C-DN的侧面积S3=π•DN•CD=
| 3 |
| 2 |
∴S表=S1+S2+S3=（15+4
| 3 |
点评：本题考查以腰BC所在直线为轴旋转一周所形成的旋转体的表面积，考查学生的计算能力，比较基础．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
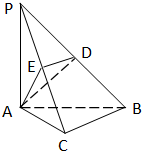如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D、E分别是棱PB、PC的中点．