题目内容
13.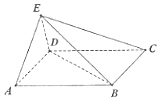 如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°
如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°(1)求证:平面ABE⊥平面ADE
(2)求点A到平面BDE的距离.
分析 (1)证明:AB⊥平面ADE,利用面面垂直的判定定理,证明平面ABE⊥平面ADE
(2)利用等体积方法,求点A到平面BDE的距离.;
解答 (1)证明:∵ABCD是正方形,∴AD⊥CD,
∵AE⊥平面CDE,CD?平面CDE,∴AE⊥CD,
∵AD∩AE=A,∴CD⊥平面ADE,
∵CD∥AB,
∴AB⊥平面ADE,
∵AB?平面ADE,∴平面ABE⊥平面ADE.
(2)解:∵AE⊥平面CDE,DE?平面CDE,∴AE⊥DE,
∵∠DAE=30°,AD=2,∴DE=1,AE=$\sqrt{3}$,
∵AB⊥平面ADE,
∴AB⊥AE,AB⊥DE,
∴BE=$\sqrt{7}$,BD=2$\sqrt{2}$,
∴DE2+BE2=BD2,
∴BE⊥DE,
设点A到平面BDE的距离为h,则$\frac{1}{3}×\frac{1}{2}$×AE×DE×AB=$\frac{1}{3}×\frac{1}{2}×$BE×DE×h,
∴h=$\frac{\sqrt{3}×2}{\sqrt{7}}$=$\frac{2\sqrt{21}}{7}$.
点评 本题考查线面垂直、面面垂直的判定,考查点面距离的计算,考查体积的计算,属于中档题.

练习册系列答案
相关题目
3.已知△ABC的内角A,B,C的对边分别是a,b,c,若A=$\frac{π}{3}$,则$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{bc}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
1.在△ABC中,AB=2,BC=$\sqrt{10}$,cosA=$\frac{1}{4}$,则AB边上的高等于( )
| A. | $\frac{3\sqrt{15}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{15}}{2}$ | D. | 3 |
13.若向量$\vec a=(1,λ,2),\vec b=(2,-1,2)$,且$\vec a$与$\vec b$的夹角余弦为$\frac{8}{9}$,则λ等于( )
| A. | -2或$\frac{2}{55}$ | B. | -2 | C. | 2 | D. | 2或$-\frac{2}{55}$ |
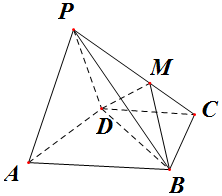 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.