题目内容
17.已知函数f(x)=2sin(-2x+θ)(0<θ<π),$f({\frac{π}{4}})=-1$,则f(x)的一个单调递减区间是( )| A. | $({-\frac{5π}{12},\frac{π}{12}})$ | B. | $({\frac{π}{12},\frac{7π}{12}})$ | C. | $({-\frac{π}{6},\frac{π}{3}})$ | D. | $({-\frac{π}{12},\frac{5π}{12}})$ |
分析 根据$f({\frac{π}{4}})=-1$,求出θ,可得f(x)的解析式,化简后,根据正弦函数的性质可得单调递减区间.
解答 解:函数f(x)=2sin(-2x+θ)(0<θ<π),
∵$f({\frac{π}{4}})=-1$,即2sin(-$\frac{π}{2}$+θ)=-2cosθ=-1,可得cosθ=$\frac{1}{2}$,
∵0<θ<π,
∴θ=$\frac{π}{3}$,
那么f(x)═2sin(-2x+$\frac{π}{3}$)=-2sin(2x-$\frac{π}{3}$),
由$-\frac{π}{2}+2kπ≤$2x-$\frac{π}{3}$$≤\frac{π}{2}+2kπ$,
得:$-\frac{π}{12}+kπ$≤x≤$\frac{5π}{12}+kπ$,k∈Z.
因此f(x)的一个单调递减区间[$-\frac{π}{12}$,$\frac{5π}{12}$],
故选D.
点评 本题主要考查对三角函数的计算能力和三角函数的图象和性质的运用.属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
7.已知sin($\frac{π}{3}$-α)=$\frac{1}{3}$,则sin($\frac{π}{6}$-2α)=( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $±\frac{7}{9}$ | D. | $-\frac{2}{9}$ |
9.已知F是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,过点F作E的一条渐近线的垂线,垂足为P,垂线PF与E相交于点Q,记点Q到E的两条渐近线的距离之积为d2,若|FP|=2d,则该双曲线的离心率( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
17.直线l的方程为2x-y=0是“直线l平分圆(x-1)2+(y-2)2=1的周长”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
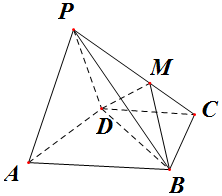 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.